Fluides visqueux
Viscosité et dissipation
Pour un fluide dissipatif, il nous faut revenir à l'expression de la dissipation (<) que nous réécrivons sous la forme
ø = σijv Dij σij = − p(ρ) δij + σijv
A la pression p(ρ) du fluide parfait vient s'ajouter une contrainte visqueuse σijv que l'on peut interpréter comme la résistance du fluide à la vitesse de déformation Dij qui lui est imposée. Le plus simple est de supposer que cette contrainte visqueuse dépend linéairement de la vitesse de déformation, relation qui en général s'écrira sous la forme
σijv = λ Dkk δij + 2μ Dij
où λ et μ sont deux coefficients de viscosité. C'est en fait un premier exemple très simple d'application des relations d'Onsager qui seront présentées plus en détail plus loin (>) . La « démonstration » de cette relation, ou plus exactement les hypothèses qui y conduisent, dépassent le cadre de ce cours ; nous aurons l'occasion d'y revenir plus loin.
On notera la très grande analogie entre ces relations et la loi de Hooke. Les coefficients λ et μ sont d'ailleurs traditionnellement notés de la même manière. Attention aux confusions lorsque plus tard nous devrons combiner les deux ; mais ce n'est pas à l'ordre du jour ici.
La dissipation doit être positive, ce qui, comme en élasticité (<) , impose
μ ≥ 0 3λ + 2μ ≥ 0
On suppose d'ailleurs souvent que le coefficient de viscosité volumique est nul (3λ + 2μ = 0).
C'est le modèle de fluide visqueux newtonien compressible. Attention toutefois, il est − contrairement aux autres modèles présentés dans cette introduction − peu pertinent d'un point de vue physique. Il n'est en effet pas très raisonnable de prendre en compte à la fois viscosité et compressibilité en négligeant les phénomènes thermiques. Un modèle physiquement raisonnable devra ici inclure les couplages thermomécaniques.
Fluide visqueux incompressible
Dans le cas incompressible ces équations se simplifient considérablement : la pression p est maintenant, comme pour le fluide parfait, un multiplicateur de Lagrange (et non plus donnée en fonction de ρ par une équation d'état) et, puisque Dii = 0, le coefficient λ disparaît. Il reste donc simplement
σij = − p δij + 2μ Dij
C'est le modèle classique du fluide visqueux newtonien incompressible. En reportant dans l'équation du mouvement (<) il vient
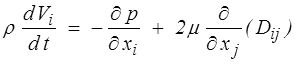
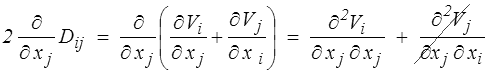
Le second terme disparaît du fait de l'incompressibilité (∂Vj /∂xj = 0). On obtient ainsi
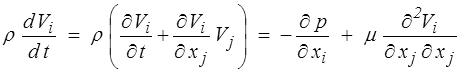
Soit, dans le cas stationnaire,
Equations de Navier-Stokes.
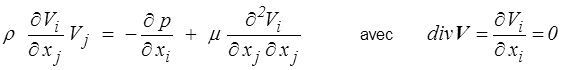
Cette équation (c'est l'équation de base en mécanique des fluides) est non-linéaire par le terme convectif d'accélération. C'est ce qui en fait toute la difficulté − tant d'un point de vue théorique que numérique.
Lorsque les vitesses sont faibles, ce terme peut parfois être négligé et on obtient les équations de Stokes très proches des équations de l'élasticité.
