Fluides parfaits
Cadre général
Contrairement à la mécanique des solides, naturellement lagrangienne, la mécanique des fluides est eulérienne. Dans une soufflerie par exemple, les « tubes de Pitot »(w) permettent la mesure des vitesses en un point donné de l'espace.
La loi fondamentale se traduit toujours par l'équation du mouvement (<)
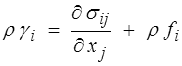
mais l'accélération, dérivée temporelle de la vitesse, sera maintenant calculée comme dérivée particulaire (l'accélération est la dérivée de la vitesse d'une particule) (<) . On écrira donc
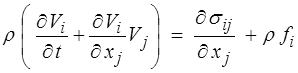
et même pour un écoulement stationnaire (<) il faut prendre en compte l'accélération.
Dans le contexte purement mécanique qui nous intéresse ici, les inconnues du problème sont les champs eulériens
- V(x,t) vitesse,
- ρ(x,t) masse volumique,
- σ(x,t) contraintes,
soit 10 quantités scalaires. L'équation du mouvement fournit 3 équations et nous devons aussi écrire l'équation de continuité (<)
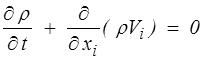
Manquent donc, comme en mécanique des solides, les 6 équations que nous donnera la loi de comportement reliant les contraintes à l'écoulement.
Calcul de la dissipation
Le premier principe combiné au théorème de l'énergie cinétique donne, comme nous l'avons vu plus haut (<) ,
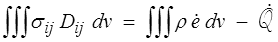
On remarquera au passage que l'on a ici sans le dire explicitement utilisé le théorème de Reynolds (<)
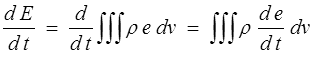
où e est l'énergie interne spécifique (densité massique). Pour l'élément de volume le bilan devient donc
σij Dij = ρ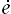
+ ø ø ≥ 0
Pour un fluide on supposera l'énergie interne spécifique e fonction de la masse volumique ρ
e = e(ρ)
Rappelons qu'en thermodynamique un fluide est défini par son énergie interne U fonction de l'entropie S, absente dans le cadre mécanique qui nous intéresse ici, et du volume V = 1/ρ puisque pour l'unité de masse m = 1 = ρV.
Pour calculer 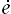on utilise l'équation de continuité (<) et on remarque que
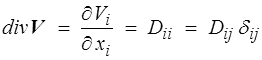
de sorte que
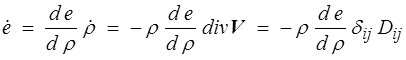
La dissipation ø sera donc donnée par
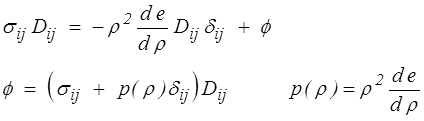
Fluide parfait barotrope
Le fluide parfait est un fluide qui ne dissipe pas d'énergie. C'est en mécanique des fluides l'analogue du modèle élastique (<) . La dissipation devant être nulle pour tout mouvement, donc toute valeur de Dij, il vient
C'est le modèle du fluide parfait barotrope (le modèle complet s'obtiendrait en prenant en compte température et entropie). Le tenseur des contraintes se réduit à une pression hydrostatique. En remarquant que pour l'unité de masse ρ = 1/V on retrouve bien la relation thermodynamique classique p = − ∂U/∂V.
En reportant dans l'équation du mouvement on obtient l'équation d'Euler
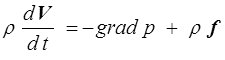
Cette équation, combinée à l'équation de continuité, donne le système
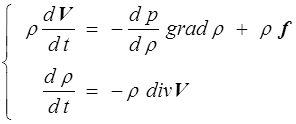
C'est le modèle de base de l'Acoustique (étude des petits mouvements d'un fluide). On fait alors l'hypothèse des petites perturbations (<) qui permet en particulier de remplacer les dérivées particulaires par des dérivées partielles. Les dérivées spatiales et temporelles commutent. Si l'on s'intéresse par exemple à la masse volumique ρ, on obtient en dérivant et combinant les deux équations ( f = 0 )
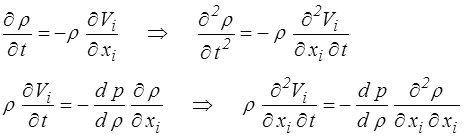
donc finalement
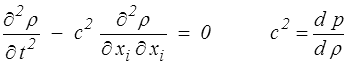
et on retrouve bien l'équation des ondes et la vitesse du son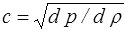 
.
C'est l'équation de base de l'Acoustique.
Fluide parfait incompressible
Si l'on suppose de plus le fluide incompressible, alors (<)
div V = Dii = 0
et la masse volumique reste constante. La dissipation ø devra être nulle pour tout tenseur Dij de trace nulle ; il faut donc introduire un multiplicateur de Lagrange et la loi de comportement s'écrira donc
σij = − p δij
On ne se laissera pas abuser par la similitude formelle avec le cas compressible. La pression p est ici une inconnue du problème qui devra être obtenue par résolution d'un problème aux limites
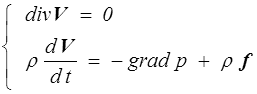
avec des conditions aux limites qui s'écriront par exemple
- p = 0 sur une surface libre,
- V . n = 0 sur une paroi fixe.
Cette dernière condition autorise le glissement du fluide à la paroi (condition de glissement).
La puissance des efforts intérieurs est nulle. C'est (avec le solide rigide) le seul modèle de mécanique des milieux continus énergétiquement neutre.
Pour un écoulement stationnaire (<) , l'accélération, dérivée particulaire de la vitesse, sera donnée par
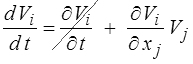
Considérons une ligne de courant (<), enveloppe du vecteur vitesse, on peut écrire pour toute fonction φ
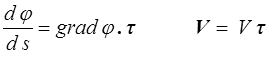
où s est l'abscisse curviligne et τ est le vecteur unitaire tangent. Par produit scalaire de l'équation d'Euler par τ, on obtient
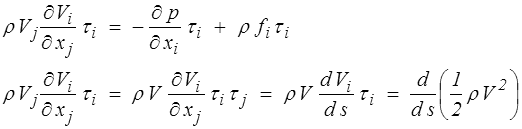
et si les forces volumiques dérivent d'un potentiel ( f = − grad u, u = gz par exemple pour un fluide pesant)
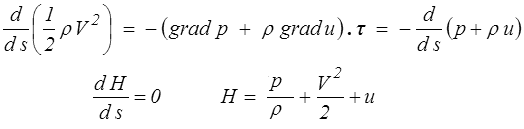
La quantité H, souvent appelée « charge hydraulique », reste constante sur une ligne de courant. C'est le théorème de Bernoulli (ou tout au moins sa variante la plus simple). (w)