Formulation d'un problème
Les équations du champ
Nous avions dressé, après avoir introduit le tenseur des contraintes, un premier bilan (<) : la MMC introduit comme inconnues
- le champ cinématique, en HPP le vecteur déplacement u(x,t)
- le champ de contraintes σ(x,t)
donc 9 = 3 + 6 inconnues (5 = 2 + 3 dans le cas bidimensionnel), tandis que la loi fondamentale se traduit par l'équation du mouvement
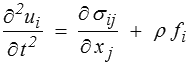
soit 3 équations (2 en bidimensionnel). Il manque 6 équations (3 en bidimensionnel).
Rappelons que, comme nous l'avons indiqué plus haut, nous avons pris acte de la symétrie du tenseur des contraintes bien que, en réalité, cette symétrie découle, au même titre que l'équation du mouvement, de la loi fondamentale. Il serait donc plus cohérent (mais nous ne le ferons pas) de considérer 12 = 3 + 9 inconnues (6 = 2 + 4 en 2D) vérifiant l'équation du mouvement (3 équations) et l'équation du moment cinétique (3 équations) qui, ici, se réduit à la symétrie du tenseur des contraintes.
C'est la loi de comportement, traduction mathématique des propriétés physiques du matériau, qui nous fournira ces équations manquantes permettant ainsi de fermer le système.
Conditions initiales
On se retrouvera alors avec un problème d'équations aux dérivées partielles par rapport aux variables d'espace x et au temps t. Il faudra alors, pour pouvoir résoudre ce problème, connaître les fonctions inconnues et/ou certaines de leurs dérivées aux frontières du domaine d'étude. On distinguera
- les conditions aux limites pour les frontières spatiales du domaine (variable x)
- les conditions initiales pour la variable temps.
Si les premières sont relativement délicates à écrire, les secondes, elles, ne posent guère de problème : comme toujours en mécanique, il faut connaître à un instant donné, que nous prendrons comme origine des temps (t = 0), la position et la vitesse du système. Les conditions initiales seront simplement
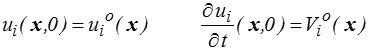
Problèmes quasi statiques
On s'intéresse souvent en mécanique des solides aux situations d'équilibre, c'est-à-dire indépendantes du temps. Les déplacements et les contraintes ne dépendent alors plus que de x, et la loi fondamentale se ramène aux équations d'équilibre
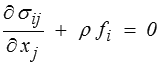
qui, complétées par des conditions aux limites, permettront de déterminer la solution ui(x), σij(x).
Plus généralement, on s'intéressera très souvent à des systèmes en évolution, mais pour lesquels les mouvements sont suffisamment lents pour que l'on puisse, dans les équations du mouvement, négliger le terme d'accélération. On retrouve alors les équations d'équilibre et l'on n'a plus besoin de conditions initiales. On parlera alors de problème quasi statique, et la solution ui(x;t), σij(x;t) dépend paramétriquement du temps. On pourrait parler d'un problème statique évolutif, l'évolution pouvant résulter des sollicitations imposées (en général par l'intermédiaire des conditions aux limites) ou parfois de la loi de comportement.
C'est dans ce cadre que nous développerons, sauf mention explicite du contraire, la suite de ce cours.
