Les équations du mouvement
La loi fondamentale
Maintenant que nous savons, grâce au Postulat de Cauchy (<), caractériser les efforts (extérieurs), nous pouvons écrire pour un domaine matériel quelconque D le principe fondamental de la dynamique (<)
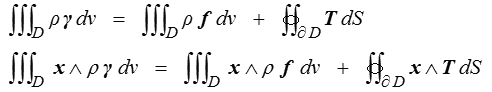
L'accélération découle directement de la description du mouvement(inconnue première de la MMC) qui, rappelons-le, sera décrit
- en description lagrangienne, par la fonction x(X, t) qui donnera γ par double dérivation, (<)
- en description eulérienne, par la fonction V(x, t), dont on déduira l'accélération par dérivée particulaire (<).
Les efforts de volume f sont connus et donnés en tout point.
Outre la position, les efforts surfaciques T dépendent de la normale n (<). La loi fondamentale, et plus précisément son équation de résultante, va nous permettre de préciser cette dépendance.
Principe d'action-réaction
Comme premier exemple considérons le domaine ci-contre : disque peu épais de section circulaire de rayon a et d'épaisseur h (h << a) et appliquons-lui l'équation de résultante. Les intégrales de volume sont en O(ha2) tandis que les intégrales de surface sont en O(a2) ou O(ha). Elles seront donc négligeables si le domaine est suffisamment petit.
(Techniquement, il faudrait se placer en un point donné, considérer des disques centrés en ce point, en faire tendre les dimensions vers zéro et invoquer la continuité des fonctions, mais ce sont là des précisions mathématiques, importantes certes dans l'absolu, mais non essentielles ici.)
Seule subsiste donc l'intégrale de surface sur la frontière de D, donc sur les trois surfaces (S+ et S−, faces supérieures et inférieures, Sl surface latérale).
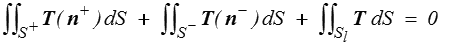
mais l'intégrale sur S + et S − sont O(a2) tandis que l'intégrale sur Sl est O(ha) et donc négligeable si h << a. Seul reste donc finalement
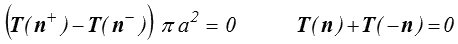
puisque n+ =−n−. On retrouve le principe d'action-réaction déjà introduit (<).
Le tétraèdre de Cauchy
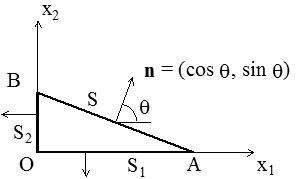
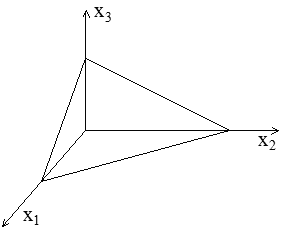
On considère ensuite
- dans l'espace tridimensionnel (à droite) un tétraèdre limité par un plan oblique et les trois plans de coordonnées,
- dans l'espace bidimensionnel (à gauche) un triangle limité par un côté oblique et les deux axes de coordonnées.
On note d la dimension du (petit) tétraèdre. Comme plus haut les intégrales de volume sont en O(d 3) (ou d 2 en 2D) et donc négligeables devant l'intégrale surfacique en O(d 2) (d en 2D).
L'intégrale de surface est la somme des quatre termes correspondant à la face oblique et aux trois faces parallèles aux plans de coordonnées (trois en 2D, la face oblique et les deux faces S1 et S2 parallèles aux axes).
Pour la clarté du dessin nous nous placerons, comme souvent dans la suite, dans le cas bidimensionnel, mais l'argumentation se transcrit mot à mot dans le cas tridimensionnel.
En remarquant que les normales extérieures sur S, S1 et S2 sont respectivement n, −e2 et −e1, il vient
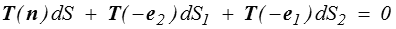
soit, compte tenu du principe d'action-réaction
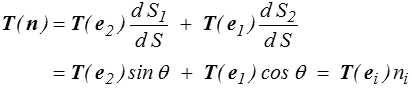
(convention de sommation (<)) où les ni sont les composantes du vecteur n (cosinus directeurs). Le résultat est donc que le vecteur contrainte T(n) dépend linéairement du vecteur normal extérieur n. Il suffit donc, pour pouvoir calculer le vecteur contrainte associé à une normale n quelconque, de connaître les vecteurs contraintes associés aux vecteurs de base ei, donc aux facettes normales aux axes de coordonnées.
Le tenseur des contraintes
On appelle tenseur des contraintes cette application linéaire. Dans le système d'axes (cartésien orthonormé) x1 x2 x3 cette application linéaire s'écrira matriciellement
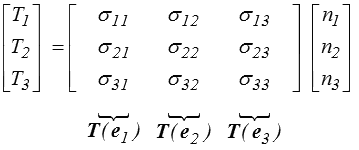
où l'on a noté (σ11, σ21, σ31 ) les 3 composantes du vecteur T(e1 ). Plus généralement on définit
σij = T(ej ) . ei
c'est-à-dire la composante i du vecteur contrainte T(ej ) associé à une facette perpendiculaire à ej .
On écrira donc
Ti = σij nj T = σ n
Ces formules permettent de calculer à partir du champ des contraintes σ(x), en tout point x et pour toute surface S, le vecteur contrainte T.
Equations du mouvement
On peut maintenant revenir à la loi fondamentale et, pour commencer, à l'équation de résultante qui, en utilisant le tenseur des contraintes, devient
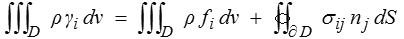
Le théorème de la divergence (<) permet de transformer l'intégrale de surface en intégrale de volume
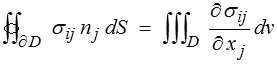
et donc de regrouper les 3 termes en
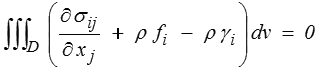
et puisque cette relation doit être vraie pour tout domaine D
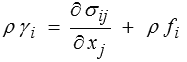
C'est l'équation du mouvement.
Dans le cas statique, c'est-à-dire lorsqu'on s'intéresse à un problème indépendant du temps, ou dans le cas quasi-statique, c'est-à-dire lorsque les évolutions temporelles sont suffisamment lentes pour que l'on puisse négliger le terme d'accélération, on obtient les équations d'équilibre
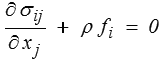
Dans le cas dynamique, il est souvent commode de conserver l'équation du mouvement sous cette forme en écrivant
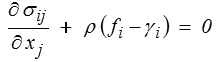
c'est-à-dire en rajoutant aux forces volumiques les « forces d'inertie » −ργi. On parle alors parfois des équations d'équilibre dynamique.
On peut aussi écrire de manière plus concise
div σ + ρ ( f − γ ) = 0
introduisant le vecteur div σ, divergence du tenseur σ. On remarque qu'il s'agit d'une équation vectorielle (3 composantes, 2 dans le cas 2D) et que le terme div σ fait intervenir la somme de 3 termes (sommation en j ). Cette notation est certes très élégante, mais son utilisation implique quelques précautions. Je la déconseille au débutant.
Moment cinétique
L'équation de conservation du moment cinétique, qui correspond à la partie moment de la loi fondamentale, s'écrit
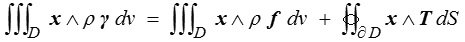
En introduisant les symboles de Levi-Civita (<) ∈ijk, le dernier terme s'écrit, en notations indicielles,
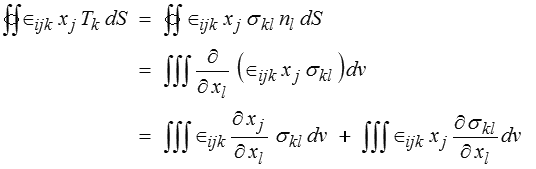
de sorte que l'on obtient finalement
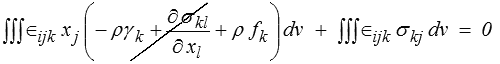
Le premier terme disparaît du fait de l'équation du mouvement et il reste finalement
∈ijk σkj = 0 σij = σji
Théorème.
Le tenseur des contraintes est symétrique.
C'est un résultat très simple, tellement simple qu'il paraît naturel, et il est tentant d'oublier son origine. Conservons bien à l'esprit qu'il s'agit en fait aussi d'une équation d'équilibre. Ce ne sera d'ailleurs plus vrai dans le cas de la MMC généralisée. Une remise en cause du postulat de Cauchy conservera en général la notion de tenseur de contrainte et les équations d'équilibre, mais avec un tenseur des contraintes non symétrique.
Un premier bilan
Pour formuler, puis résoudre, un problème de MMC nous devons donc déterminer à chaque instant :
- le mouvement du système, c'est-à-dire les champs x(X, t) ou V(x, t) suivant que nous avons choisi la description lagrangienne ou eulérienne (donc 3 composantes),
- le champ de contraintes σ(x, t) (ou σ(X, t), mais dans la suite nous laisserons provisoirement de côté cette possibilité), soit 6 composantes (en fait 9, mais comme suggéré plus haut nous prenons désormais pour acquis la symétrie du tenseur des contraintes).
Face à ces 9 inconnues nous disposons des 3 équations du mouvement données par la loi fondamentale. Il nous manque donc 6 équations, qui seront spécifiques et prendront en compte la nature physique du matériau (air, eau, huile, glace, bitume, acier, béton,...). Ce sera la loi de comportement qui reliera les contraintes au mouvement.