Mécanique des Milieux Continus
Description lagrangienne
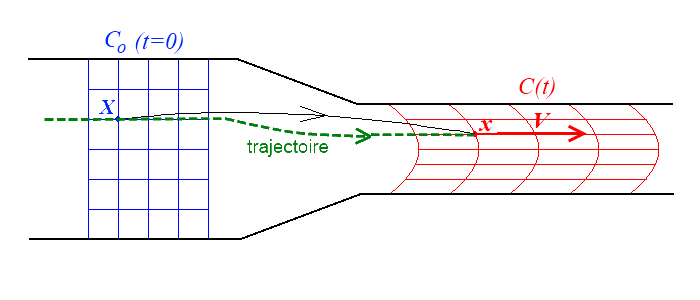
Le modèle de la MMC (Mécanique des Milieux Continus) considère que la matière occupe l'espace de manière continue et donc qu'à chaque instant une « particule » est associée à chaque point de l'espace occupé à cet instant par la matière. La description la plus naturelle du mouvement consiste donc à se donner à chaque instant t la position x de la particule qui, dans une configuration choisie comme référence, occupe la position X.
Description lagrangienne.
x = x(X, t)
On prend en général comme configuration de référence la configuration du système au temps t = 0. Cela n'a rien d'obligatoire, et l'on peut tout à fait choisir comme référence une configuration abstraite qui n'a jamais été et ne sera jamais occupée par le système ; cela ne changerait pas grand-chose, mais je propose pour fixer les idées de nous limiter à ce cas. Il convient, par contre, de conserver présent à l'esprit le fait que ces variables lagrangiennes Xi , i = 1,..3 représentent davantage un identificateur de particule plutôt qu'une position.
Cette fonction x(X, t) sera dans la suite supposée continue, inversible en une fonction
X = X(x, t)
donnant la position initiale de la particule qui, à l'instant t, se trouve en x. Elle sera aussi suffisamment régulière pour que les calculs qui suivront soient légitimes.
On définit alors traditionnellement
- la trajectoire d'une particule Xo, ensemble des positions occupées au cours du temps par cette particule
x = x(Xo, t) Xo fixé, t varie,
- les lignes d'émission, ensemble des positions à l'instant t de toutes les particules qui sont passées ou passeront au point xo
x = x(X(xo, τ), t) xo, t fixés, τ varie.
La MMC, pour quoi faire ?
Par opposition à la mécanique du solide rigide (<), la MMC est la mécanique des milieux déformables − et la description des déformations en sera plus loin une étape importante −
- Pour étudier l'écoulement d'un fluide (Aérodynamique, Hydrodynamique) ou même ses petits mouvements (Acoustique), c'est bien évidemment indispensable.
- Dans le cas des solides c'est beaucoup moins évident. Si l'on observe par exemple une table sur laquelle est posé un objet lourd, la déformation de la table n'est sans doute pas nulle, mais restera très faible et donc − pourrait-on penser − tout-à-fait négligeable, et bien non !
- Tout d'abord il peut exister des cas où ces petits écarts sont fonctionnellement importants : on peut par exemple imaginer un dispositif de surveillance basé sur la réflexion d'un rayon laser sur le plateau de la table. C'est en fait le principe de mesure du microscope à force atomique (w).
- Ensuite c'est la prise en compte des déformations − bien qu'elles soient très petites − qui permettra de résoudre des problèmes insolubles dans le cadre de l'hypothèse d'un solide rigide, par exemple calculer les efforts transmis par chacun des quatre pieds de la table.
- Enfin et surtout, c'est la MMC qui permettra de calculer les efforts intérieurs, qui conditionnent la résistance, les risques de rupture ou la durée de vie.
On peut également s'interroger sur la pertinence et/ou la nécessité de cette description que l'on sait être fausse à l'échelle atomique : la matière n'est pas continue et le modèle du système de particules (<) montre comment on devrait pouvoir l'aborder : il "suffit" de résoudre les 3N équations différentielles évoquées plus haut. Mais N est très grand (6*1023 par mole typiquement, nombre d'Avogadro). En fait les calculs de dynamique moléculaire, mise en oeuvre numérique de ce modèle, sont actuellement limités à quelques milliers d'atomes. On cite un calcul portant sur 1 million d'atomes pendant 50 ns (!! de temps simulé, le temps nécessaire au calcul n'est pas donné, mais il se compte sans doute en semaines ! ).
Au contraire la MMC n'introduira qu'un faible nombre (9 ou 10 en fait) de fonctions inconnues mais, outre l'approximation elle-même, cette simplification a un prix : car ce seront des fonctions de 4 variables (t, x) au lieu de 3N fonctions d'une seule variable. Les équations différentielles deviendront donc des équations aux dérivées partielles avec les difficultés mathématiques qui en résultent.
C'est une théorie du champ et, comme on peut s'y attendre, les vecteurs et les tenseurs y jouent un rôle essentiel ===>.
Description eulérienne
La vitesse d'une particule V(X, t) est bien évidemment la dérivée par rapport au temps de sa position
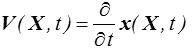
En général toutefois on observera ou mesurera cette vitesse en un point donné de l'espace x. Le champ eulérien des vitesses est donné par
V(x, t) = V(X(x, t), t)
donnant à chaque instant la vitesse de la particule en fonction de la position x qu'elle occupe à l'instant t considéré.
Description eulérienne.
V = V(x, t)
Ces deux descriptions, lagrangienne et eulérienne, sont équivalentes : on vient de voir comment passer du lagrangien à l'eulérien. Réciproquement en partant de la description eulérienne on remontera à la description lagrangienne par intégration du système différentiel
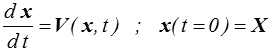
En mécanique des solides il est en général relativement naturel de marquer les particules, la description lagrangienne est naturelle, alors qu'en mécanique des fluides on observe plutôt l'écoulement, ce qui conduit naturellement à la description eulérienne.
On définit les lignes de courant comme les enveloppes, à chaque instant, du champ des vecteurs vitesses.
Définition.
Un écoulement sera dit stationnaire si le champ des vitesses ne dépend pas explicitement du temps
V = V(x)
On montre alors simplement que trajectoires, lignes d'émission et lignes de courant coïncident.
Dérivées particulaires
Considérons une grandeur scalaire, par exemple la température θ. Elle dépendra, en MMC, du temps et du point considéré (champ de température), mais on peut là encore choisir la description lagrangienne θ(X, t) rattachant la température à une particule (cas d'un thermocouple immergé dans un solide en mouvement), ou la description eulérienne θ(x, t) attachée à un point de l'espace (thermocouple fixé dans une soufflerie). Les dérivées (partielles) par rapport au temps seront bien évidemment différentes dans ces deux descriptions.
En général ces dérivées temporelles interviendront pour l'écriture de lois physiques et concerneront donc un système matériel, c'est-à-dire lié à un ensemble de particules. La dérivée devra donc être calculée en suivant les particules dans leur mouvement. C'est la dérivée particulaire notée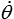 
ou d θ / d t.
En description lagrangienne cela se fait automatiquement puisque la dérivée partielle se fait alors à X constant, donc à particule fixe,
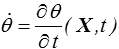
En description eulérienne par contre, il faut prendre en compte le mouvement de la particule en écrivant
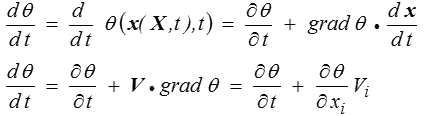
où l'on a, dans la seconde écriture, utilisé les notations indicielles et la convention de sommation (<).
De la même manière l'accélération est, pour une particule, la dérivée de la vitesse par rapport au temps: γ = d V / dt. En description lagrangienne c'est toujours la dérivée partielle
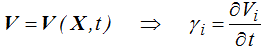
tandis qu'en description eulérienne il faut encore prendre en compte pour chaque composante le mouvement de la particule.
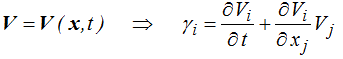
Il en résulte en particulier que pour un écoulement stationnaire (<) − et bien que la vitesse ne dépende pas du temps − l'accélération n'est pas nulle.
Théorème de Reynolds
Considérons de la même manière une grandeur physique définie par une intégrale de volume. Là encore on pourra définir, suivant que l'on utilise la description lagrangienne ou eulérienne,
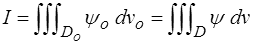
où ψ(o [resp. ψ] représente une densité par unité de volume lagrangien [resp. eulérien]. Pour dériver par rapport au temps cette intégrale on pourra, en description lagrangienne, dériver sans scrupule sous le signe somme
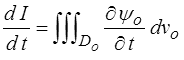
alors que, en description eulérienne, il est nécessaire de prendre en compte le fait que le domaine D change au cours du temps. Dans la dérivée d I / d t on aura donc deux termes provenant
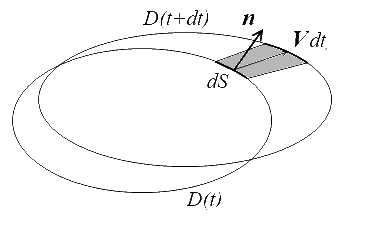d'une part de la variation de la quantité ψ à l'intérieur du domaine,- d'autre part de l'évolution du domaine D (rajouter ce qui rentre et supprimer ce qui sort). La contribution à cette variation du domaine hachuré sera simplement le produit de la valeur de la fonction ψ au point M par le volume de ce domaine Vdt.ndS ( V.n > 0 si les particules sortent du domaine, à droite sur la figure, V.n < 0 si elles y rentrent).
On pourra donc écrire
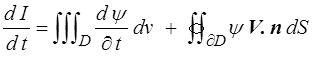
ou, en utilisant le théorème de la divergence (<) ,
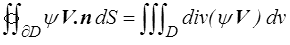
Théorème de Reynolds.
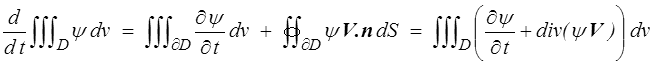
Comme premier exemple on peut prendre ψ = 1 et calculer ainsi la variation du volume occupé par un ensemble de particules
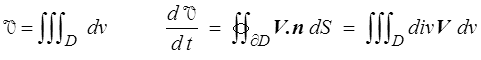
En particulier, un matériau sera dit incompressible si ce volume ne peut pas changer, ce qui se traduit par
div V = 0
Equation de continuité
On peut appliquer ce résultat pour écrire que la masse d'un domaine matériel reste constante
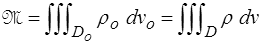
où ρ et ρo représentent la masse par unité de volume dans C(t) et Co respectivement (masse volumique).
En description lagrangienne on obtient simplement
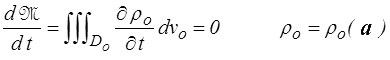
La masse volumique dans la configuration de référence peut dépendre de la particule (hétérogénéité), mais pas du temps.
En description eulérienne le théorème de Reynolds donne
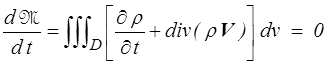
Ceci devant être vrai pour tout domaine matériel on en déduit
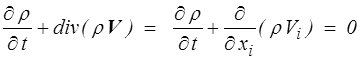
On peut aussi écrire cette équation sous la forme
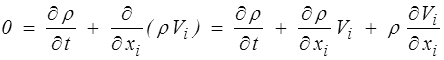
et on reconnaît dans les deux premiers termes la dérivée particulaire de la masse volumique ρ. On obtient donc une forme équivalente
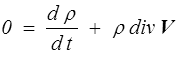
Equation de continuité.
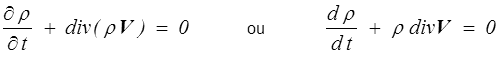
C'est la traduction eulérienne de la conservation de la masse.
Question : mais puisque c'est si simple en description lagrangienne, pourquoi s'embêter avec l'eulérienne ? Cette question nous servira de point de départ pour attaquer les grandes transformations. En attendant, je vous laisse la méditer..
Ce résultat permet de simplifier considérablement le théorème de Reynolds. On part maintenant de
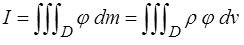
introduisant la densité par unité de masse φ (plutôt que par unité de volume, ψ = ρφ). On peut alors écrire (bon exercice d'application pour se familiariser avec les notations indicielles)
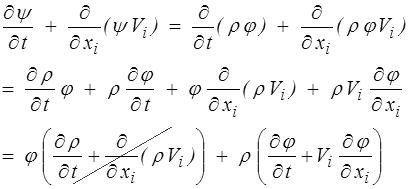
Le premier terme disparaît (c'est l'équation de continuité), tandis que l'on reconnaît au second terme la dérivée particulaire de φ
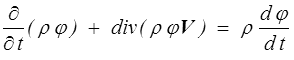
Le théorème de Reynolds se ramène donc à
Théorème de Reynolds - Deuxième forme.
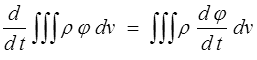
On peut encore dériver sous le signe somme mais à condition de travailler par unité de masse (qui, elle, se conserve ; c'est donc au fond bien naturel).
Remarquons pour terminer que tout cela suppose les fonctions dérivables, et interdit donc les discontinuités (ondes de chocs). Pour les prendre en compte, il faudra étendre ces résultats en les complétant par des équations de saut devant être vérifiées au travers de ces discontinuités. Nous les laisserons de côté dans ce cours.