Elasticité linéaire
Tenseur d'élasticité
Dans notre présentation initiale monodimensionnelle nous avons écrit que σ était proportionnel à ε. Dans le cas tridimensionnel nous écrirons que le tenseur des contraintes dépendra linéairement du tenseur des déformations. L'énergie de déformation w(εij ) devra donc être une forme quadratique qui, en général, s'écrira
w = ½ Aijkl εij εkl
Le système des quantités Aijkl (où i, j, k, l peuvent prendre les valeurs 1, 2, 3, soit a priori 81 quantités) définissent ce que l'on appelle le tenseur d'élasticité du matériau (tenseur du quatrième ordre (<) ; que le lecteur ne s'effarouche toutefois pas, ce n'est qu'une question de vocabulaire sans grande importance ici).
Le tenseur des déformations étant symétrique, ce système doit vérifier les conditions de symétrie
Aijkl = Ajikl = Aijlk
et de plus, puisque w est une forme quadratique,
Aijkl = Aklij
Ces relations de symétrie réduisent à 21 le nombre de composantes indépendantes (le lecteur courageux peut le vérifier, mais je lui conseille plutôt d'attendre le cours de Comportement des Matériaux où nous écrirons ces relations générales sous une forme plus manipulable).
Par dérivation on obtient directement
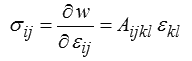
C'est la loi de comportement de l'élasticité linéaire.
Le plus simple pour démontrer ces relations est de différentier la fonction w (Un nouvel exercice de manipulation des notations indicielles et l'illustration d'une technique agréable pour calculer une dérivée, il vaut donc la peine d'y consacrer quelque attention)

d'après la dernière relation de symétrie. Ceci nous donne le résultat annoncé en identifiant avec la définition de la dérivée partielle
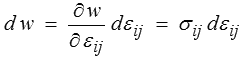
Remarquons aussi qu'un lecteur pressé aurait pu être tenté de généraliser la relation σ = E ε en une simple relation scalaire σij = E εij. Il fallait résister à cette tentation trop simpliste.
Tenseur de souplesse
L'inversion de la loi élastique donne
εij = Sijkl σkl S = A−1
où le tenseur Sijkl est, au sens des applications linéaires, l'inverse du tenseur d'élasticité
Sijkl Aklmn = Aijkl Sklmn = δim δjn
Dans la pratique, toutefois, on détermine plutôt ce tenseur par solution directe en εij du système linéaire
σij = Aijkl εkl => εkl = Sklmn σmn
Ces quantités Sijkl vérifient les mêmes symétries que Aijkl
Sijkl = Sjikl = Sijlk Sijkl = Sklij
Elles définissent le tenseur de souplesse ou tenseur de complaisance − compliance en anglais, et vous trouverez (malheureusement) ce terme en français aussi.
Quant à l'énergie complémentaire w c, on l'obtient directement à partir de sa définition
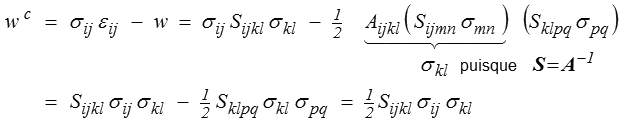
qui, par dérivation, donne bien évidemment la relation écrite ci-dessus. On peut donc écrire
w c = ½ Sijkl σij σkl = ½ σij εij = ½ Aijkl εij εkl = w
Dans ce cas particulier, mais dans ce cas seulement, l'énergie complémentaire est égale à l'énergie
w ( εij ) = w c( σij ) = ½ σij εij
relation séduisante, mais dangereuse car fausse sitôt que l'on quitte le cas linéaire.
De par la condition de Stabilité (<), ces deux formes quadratiques sont définies positives
Identification de la loi élastique
La loi élastique fait donc intervenir 21 coefficients, les constantes élastiques du matériau, et, comme pour toute loi de comportement, ces coefficients doivent être déterminés expérimentalement.
En principe tout semble simple, il suffit de réaliser 6 essais imposant chacun une seule composante du tenseur des contraintes, la mesure des 6 composantes de la déformation donnant alors 6 composantes du tenseur S.
Par exemple en traction simple

et on ne retrouve pas du tout ce qu'on avait annoncé (<) lorsque nous avons introduit cet essai. Nous nous étions en fait limités au cas isotrope, et, dans le cas général, la situation est beaucoup plus complexe. L'identification des constantes élastiques pose en général des problèmes difficiles. Nous y reviendrons dans le cours de Comportement des Matériaux.
