Le tenseur des contraintes
Les efforts de cohésion sont donc caractérisés par une application linéaire symétrique, le tenseur des contraintes. Il devrait s'agir là, pour la plupart des lecteurs non initiés, d'un concept radicalement nouveau (<). La physique nous a déjà donné maints exemples de grandeurs physiques vectorielles. Sauf cas particulier, ce devrait être la première fois que vous rencontrez une grandeur physique première représentée par une application linéaire.
Les composantes du tenseur des contraintes
Une fois choisi un repère orthonormé, le tenseur des contraintes sera défini par ses composantes σij (9 dont 6 indépendantes en 3 dimensions, 4 dont 3 indépendantes en 2 dimensions ; comme précédemment nous limiterons souvent nos représentations géométriques à ce cas).
Ces composantes sont en fait, comme nous l'avons vu plus haut, les composantes des vecteurs contraintes appliqués sur les facettes normales aux axes.
Cette interprétation est rappelée sur la figure suivante
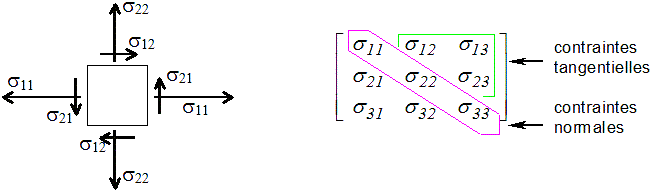
Il en résulte en particulier que les composantes diagonales représentent des contraintes normales, tandis que les composantes en dehors de la diagonale représentent des contraintes tangentielles ou de cisaillement (<) .
Il en résulte également que la symétrie du tenseur des contraintes implique que les contraintes tangentielles exercées sur deux faces perpendiculaires sont égales. C'est pour cela qu'on parle souvent, pour indiquer la symétrie du tenseur des contraintes, de «réciprocité des cisaillements».
Changement de repère
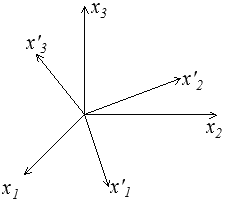Les composantes du tenseur des contraintes dépendent bien évidemment du repère choisi.
Considérons donc deux repères (e1 , e2 , e3 ) et (e'1 , e'2 , e'3 ).
On passe de l'un à l'autre par une matrice de passage Qij
e'i = Qij ej
et si de plus les deux repères sont orthonormés cette matrice est orthogonale (c'est-à-dire que son inverse est sa transposée)
Qij Qil = δjl Q QT = QT Q = 1
Les formules de changement de repère pour un vecteur, le vecteur contrainte par exemple, s'obtiennent simplement (<).
T'i = Qij Tj ou Ti = Q ji T'j
Pour obtenir les formules de changement de repère pour le tenseur des contraintes, on part de la relation T = σ n écrite dans les deux repères
Qij Tj = T'i = σ'ij n'j = σ'ij Q jk nk
Tm = Qij Qim Tj = Qim Q jk σ'ij nk = σmk nk
d'où l'on tire
σmk = Qim Q jk σ'ij σ'ij = Qik Q jl σkl
Déviateur et partie sphérique
Il est souvent utile (bien que la signification physique nous en échappe encore) de décomposer le tenseur des contraintes en partie sphérique et déviateur.
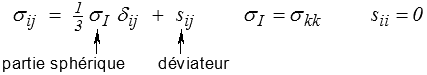
La partie sphérique correspond à une «tension» hydrostatique, c'est-à-dire un vecteur contrainte normal à la facette pour toute direction. Le déviateur est un tenseur de trace nulle (on appelle trace la somme des termes diagonaux)
tr(σ) = σii = σ11 + σ22 + σ33
Contraintes principales
La matrice représentative étant symétrique, ses valeurs propres sont réelles et il existe un repère principal orthonormé.
On note traditionnellement σ1, σ2, σ3 les valeurs propres : ce sont les contraintes (normales) principales.
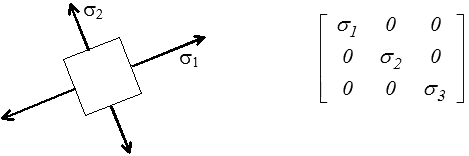
Les directions principales sont donc caractérisées par le fait que les contraintes tangentielles (termes en dehors de la diagonale) y sont nulles. En particulier une surface libre de contraintes (c'est-à-dire sur laquelle ne s'exerce aucun effort, T = 0, ce sera souvent le cas au bord d'un objet) sera toujours principale.
Remarquons que le tenseur des contraintes dépend de 6 quantités et sera donc complètement défini par les trois contraintes principales et les trois paramètres définissant l'orientation du repère principal (angles d'Euler, par exemple).
Dans le cas bidimensionnel de même, on peut choisir les deux contraintes principales et l'angle définissant l'orientation des directions principales.
Invariants fondamentaux
Pour trouver les contraintes principales d'une matrice il faut résoudre son équation caractéristique
σ n = λ n (σ − λ1) n = 0
et pour que ce système linéaire admette une solution non nulle, il faut (et il suffit) que
P(λ) = det (σ − λ1) = 0
C'est l'équation caractéristique de σ, et P(λ) est son polynôme caractéristique. C'est un polynôme du troisième degré
P(λ) = −λ3 + σI λ2 − σII λ + σIII = 0
Les coefficients σI , σII , σIII de ce polynôme sont appelés invariants principaux de σ.
Un calcul plus ou moins simple, suivant qu'on le prend plus ou moins astucieusement, montre que
σI = tr (σ) = σkk = σ1 + σ2 + σ3
σII = (σii σjj − σij σij ) / 2 = σ1 σ2 + σ2 σ3 + σ3 σ1
σIII = det σ = σ1 σ2 σ3
La terminologie invariant traduit le fait que ces quantités ne dépendent pas du repère choisi et sont donc invariantes par changement de repère, comme cela se voit directement à partir des formules de changement de repère.
Pour être tout à fait honnête c'est direct pour les deux premières, un peu moins pour la troisième, mais il peut alors être commode d'invoquer l'identité de Cayley-Hamilton (une matrice est racine de son équation caractéristique)
P(σ) = −σ 3 + σI σ 2 − σII σ + σIII 1 = 0
d'où l'on tire en prenant la trace
σIII = tr (σ 3 − σI σ 2 + σII σ) / 3
Ce sont là en fait des définitions générales applicables à n'importe quel tenseur, par exemple au déviateur des contraintes (>) . Nous n'insisterons pas davantage dans ce cours, mais nous y reviendrons(>). .