Solides déformables en HPP
L'hypothèse des petites perturbations
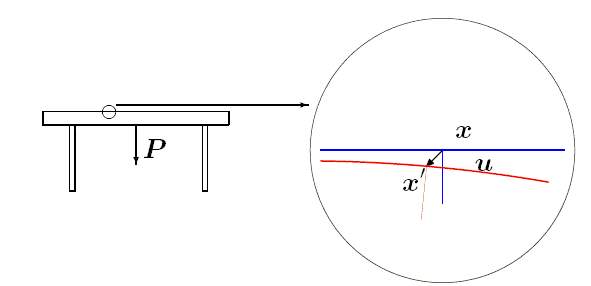
Dans les situations usuelles en calcul des structures les mouvements restent faibles et les solides s'écartent peu de leur configuration initiale de référence. On pourra donc écrire
x = X + u(X, t)
où u(X, t) est le vecteur déplacement, qui sera dans la suite supposé « petit » − ce qui n'a pour l'instant pas grand sens puisqu'il s'agit d'une longueur, donc d'une grandeur dimensionnée ; nous préciserons plus loin −.
Il en résulte que l'on pourra identifier x et X, variables lagrangiennes et variables eulériennes. C'est là à proprement parler l'Hypothèse des Petites Perturbations − HPP − (parfois appelée, notamment en Résistance des Matériaux, hypothèse de linéarité externe).
La variable x représentera indifféremment la position initiale ou finale de la particule, et sera donc considérée comme
- lagrangienne quand cela nous arrangera, notamment pour calculer les dérivées partielles temporelles ; nous pourrons donc oublier les subtilités liées par exemple à la notion de dérivée particulaire (<). En particulier l'accélération sera tout simplement la dérivée seconde du vecteur déplacement.
- eulérienne quand cela nous conviendra mieux, notamment pour écrire des lois physiques qui, bien évidemment, s'appliquent dans l'espace physique tel qu'il est à l'instant considéré.
Lorsque nous voudrons explicitement noter la position après déformation, nous la noterons désormais x'. La formule précédente devient donc, et pour ce cours,
x' = x + u(x, t)
Nous reviendrons aux notations X et x lorsque nous aborderons le cours sur les grandes transformations.
Plus techniquement, cette hypothèse nous permettra également de linéariser diverses expressions, c'est-à-dire de nous limiter à un développement du premier ordre en négligeant les termes d'ordre supérieur.
Discussion
Plutôt que de petites perturbations on parle souvent de petites déformations ou de déformations infinitésimales. Effectivement, une conséquence majeure de cette hypothèse sera, plus tard, l'introduction du tenseur des déformations infinitésimales, mais il existe de nombreux cas − notamment en théories des poutres ou des plaques − où l'on sortira du cadre des petites perturbations bien que les déformations restent petites. On devra alors développer des modèles de « petites déformations - grands déplacements ». Ces modèles, souvent présentés de manière empirique, gagnent en fait à être replacés dans le contexte général de la MMC en grandes transformations (>) .
Pour être plus précis, on pourrait caractériser cette Hypothèse des Petites Perturbations (HPP) par
Hypothèse des petites perturbations.
1. Les déplacements sont très faibles par rapport à la dimension L des solides considérés.
2. Le gradient des déplacements est petit
| u |<< L | ∂ ui / ∂ xj | << 1
Ce gradient étant une quantité sans dimension il est pertinent de le dire petit.
