Le postulat de Cauchy
Une fois introduite la description cinématique (eulérienne ou lagrangienne) d'un milieu continu en mouvement, l'étape suivante est la mise en œ ouvre, dans ce cadre, de la loi fondamentale. Pour un domaine matériel D, le torseur dynamique s'obtient par intégration des quantités d'accélération γ dm = ρ γ dv
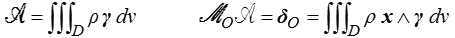
Pour avancer, il nous faut donc schématiser les efforts (extérieurs, bien sûr ; ils ne seront « intérieurs » que pour un système S dans lequel est immergé D ) exercés sur D par le monde extérieur.
Postulat de Cauchy
C'est l'hypothèse fondatrice de la mécanique des milieux continus :
Les efforts appliqués sur D sont constitués par
 |
|
Dépendance par rapport au domaine
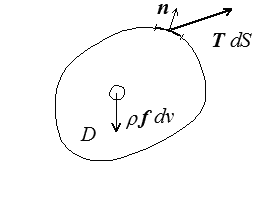
Cette densité surfacique d'efforts, appelée vecteur contrainte, dépend du point considéré x , mais aussi du domaine D. On complète traditionnellement le postulat de Cauchy en supposant que ce vecteur contrainte ne dépend du domaine D que par sa normale extérieure n
T = T(x;n)
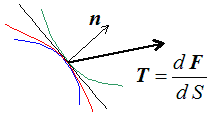En d'autres termes, on suppose que ce vecteur contrainte au point M est le même pour les surfaces représentées ci-contre.
En fait, certains travaux ont été consacrés à des tentatives de démonstration de cette propriété, et la question de savoir si cette affirmation est une hypothèse ou un théorème reste, à ma connaissance, ouverte. Il faut d'ailleurs noter que, contrairement au postulat de Cauchy lui-même, la remise en cause de cette hypothèse n'a jamais donné lieu à des développements cohérents, ce qui pour moi suggère que c'est plutôt un théorème, même si je suis bien incapable de le démontrer.
Le vecteur contrainte
Le vecteur contrainte T est une force par unité de surface et doit donc s'exprimer en Pa (Pascals) ou en MPa, mais on rencontrera hélas encore souvent des bars (1 bar = 105 Pa), des hectobars, des kilos par millimètres carrés, voire des Torr ou, dans la littérature anglo-saxonne, des « psi » (pound per square inch, 1 psi = 6894.757 Pa).
Par projection sur la normale n et sur le plan tangent à la surface
T = Tn n + Tt
on définit
- la contrainte normale Tn,
- le vecteur contrainte tangentielle ou de cisaillement Tt.
Puisque la normale n est dirigée vers l'extérieur, il en résulte que la contrainte normale est positive en traction, négative en compression. C'est la convention usuelle en mécanique des milieux continus, mais elle n'est pas universelle : en mécanique des sols, par exemple, on utilise plutôt la convention contraire, mieux adaptée aux états de compression que l'on y rencontre.
Cette décomposition est importante puisque l'on sent bien qu'un matériau donné réagira différemment à ces contraintes.
- Dans un matériau fragile comme la craie, c'est la contrainte normale qui produira la rupture, par décohésion.
- Dans un matériau métallique, ce sont les contraintes tangentielles qui piloteront, par glissement relatif des plans cristallographiques, la déformation.
Nous y reviendrons (>)
Action-Réaction
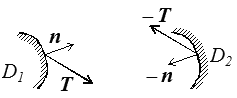En vertu du principe d'action-réaction, les efforts exercés sur D1 par son complémentaire D2 sont opposés aux efforts exercés par D2 sur D1. On en tire
T(x;n) = −T(x;−n)
Efforts extérieurs ou intérieurs ?
Comme souligné plus haut, la mécanique ne connaît en fait que les efforts extérieurs. Les soi-disant efforts intérieurs ne sont en fait que des efforts extérieurs exercés par une sous-partie du système sur la partie complémentaire.
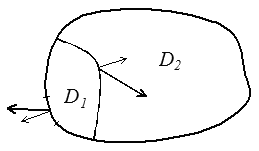Le vecteur contrainte décrira donc les efforts extérieurs comme les efforts intérieurs. N'oublions simplement pas que pour donner un sens aux efforts intérieurs il faut les « extérioriser » par une coupure du domaine.
Milieux continus généralisés
Le postulat de Cauchy est à la base de la Mécanique des Milieux Continus classiques, mais il est possible − et parfois nécessaire − de le remettre en cause pour construire des modèles de Mécanique des Milieux Continus généralisés. On peut ainsi introduire des milieux continus de Cosserat, avec couples de contraintes, au second gradient, etc...
Ces modèles, introduits au début du XXème siècle par les frères Cosserat, ont connu une grande popularité dans les années 70. Tombés dans l'oubli ensuite, ils sont redevenus d'actualité depuis une vingtaine d'années.
Parmi les applications clairement identifiées, on peut citer
- les cristaux liquides,
- les phénomènes de capillarité.
Retenons simplement que le « Postulat de Cauchy », comme beaucoup de « principes physiques », définit en fait un cadre de modélisation phénoménologique performant, efficace et en général largement suffisant, mais qu'il est parfaitement légitime, et parfois nécessaire, de le remettre en cause.