Problèmes réguliers
Pour un système d'équations aux dérivées partielles (et contrairement au cas des équations différentielles ordinaires) l'écriture des conditions aux limites est en général difficile. D'un point de vue physique, ces conditions traduisent les sollicitations imposées au bord de la pièce (on pourrait aussi envisager des sollicitations imposées à l'intérieur même de la pièce, mais il faudrait alors pouvoir agir sur les forces volumiques, ce qui, dans l'état actuel de la technologie, ressort soit de la recherche académique, soit de la science-fiction).
Pour dégager une doctrine générale, nous allons nous appuyer sur quelques exemples.
Solide immergé
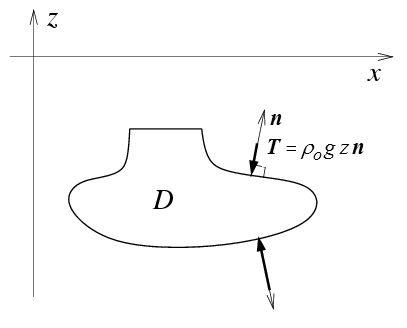Considérons un solide D immergé dans un fluide (eau par exemple). Il est soumis sur toute sa frontière à la pression de l'eau. Or les lois de l'hydrostatique (<)
nous disent que cette pression est proportionnelle à la hauteur d'eau par rapport à la surface
p = − ρo g z
où ρo est la masse volumique de l'eau, g l'accélération de la pesanteur et z la profondeur.
Sur chaque élément de la frontière S = ∂D du solide s'exerce donc une force
d f = − p n dS
On peut donc écrire comme condition aux limites
T |S = − p n = + ρo g z n
Les conditions aux limites donnent le vecteur contrainte en chaque point de la frontière.
Remarquons que, si le solide est à très grande profondeur, il pourra être légitime de négliger la variation de pression entre les divers points du solide, et on remplacera la condition précédente par
T |S = − Po n
où Po est la pression régnant à la profondeur considérée. Le problème sera alors beaucoup plus simple à résoudre.
Ce serait également le cas si le solide était plongé dans un réservoir sous pression.
Enceinte sous pression
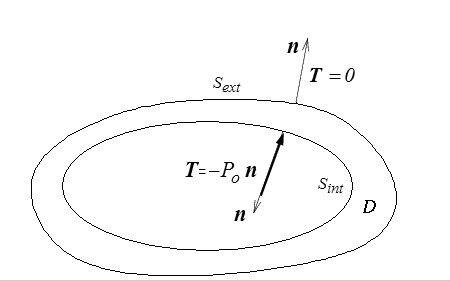Considérons une enceinte sous pression Po.
Comme précédemment la paroi interne sera soumise à cette pression
T |Sint = − Po n
La paroi externe se trouve à l'air libre (dans la vie réelle il faudrait sans doute prendre en compte également la liaison du réservoir avec le sol, mais nous ne nous en préoccupons guère ici) et est donc soumise à la pression atmosphérique.
En mécanique des solides et par convention la pression atmosphérique est nulle, ce qui revient en fait à prendre comme origine des contraintes la pression atmosphérique. C'est tout à fait naturel sur Terre puisque tous les objets sont soumis à cette pression atmosphérique. On écrira donc sur la paroi externe
T |Sext = 0
et on parlera d'une surface libre. C'est une condition aux limites très courante, au point que dans la plupart des logiciels éléments finis c'est la condition par défaut.
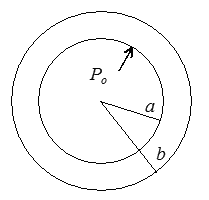Dans le cas d'une enceinte sphérique on écrira
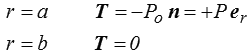
soit en utilisant les coordonnées sphériques (<)
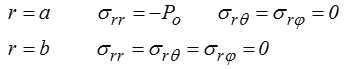
puisque la normale n est + er sur la surface externe et − er sur la surface interne.
C'est un problème classique en mécanique des milieux continus, et nous en déterminerons plus loin la solution dans quelques cas particuliers. On traitera de manière analogue le cas d'une enveloppe soumise également à une pression externe ou le cas d'une cavité sphérique dans un milieu infini.
Bloc pesant
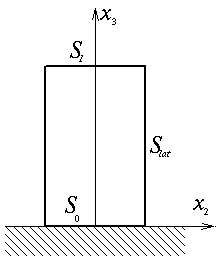Considérons maintenant un bloc pesant posé sur un massif rigide.
La surface supérieure et la surface latérale sont des surfaces libres. On écrira donc simplement
T |S1 = 0 T |Slat = 0
Par contre les conditions de contact avec la table sont moins évidentes et nécessitent des hypothèses supplémentaires sur la nature du contact.
Un premier cas simple est le cas d'un contact adhérent, interdisant tout déplacement relatif du bloc par rapport à la table. Le déplacement doit donc être nul, et la condition aux limites adaptée est
u |So = 0
annulant au contact avec la table (supposée indéformable) le déplacement des points du bloc.
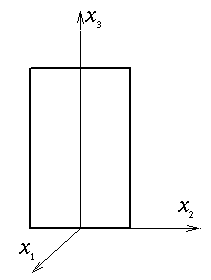Dans le cas d'un contact sans frottement, au contraire, le bloc peut glisser sur la table, et donc, si la composante verticale u3 du déplacement doit toujours être nulle pour assurer le contact (x3 verticale ascendante), les composantes horizontales u1 et u2 représentent le glissement et sont donc inconnues. Par contre le contact étant sans frottement, la réaction, c'est-à-dire en fait le vecteur contrainte, devra être normale à la surface, et donc verticale. Les conditions aux limites traduisant un contact sans frottement seront donc
sur So u3 = 0 T1 = T2 = 0
Ces deux cas sont évidemment deux idéalisations de la réalité (frottement infini dans le premier cas, frottement nul dans le second cas) et pour être plus proche de la réalité il faudrait écrire, en plus de la condition de contact u3 = 0 une relation entre les composantes horizontales du déplacement et du vecteur contrainte traduisant les conditions physiques du contact − par exemple le frottement de Coulomb. Le problème deviendrait alors beaucoup plus complexe et hors de portée dans ce cours d'introduction.
Revenons à notre problème du bloc pesant et à ses deux idéalisations ; nous verrons plus loin que malgré les idéalisations on ne pourra pas en trouver, même dans le cas le plus simple, une solution explicite.
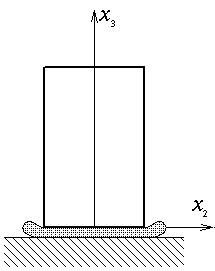Nous saurons par contre résoudre un troisième problème correspondant au cas où le contact entre le bloc et la table est réalisé au travers d'une enveloppe souple contenant un fluide qui alors impose au bloc sa pression. La condition aux limites s'écrira alors
T = − Pf n c'est-à-dire T3 = + Pf T1 = T2 = 0
où Pf est la pression du fluide. Nous pourrons alors résoudre le problème.
Un barrage poids
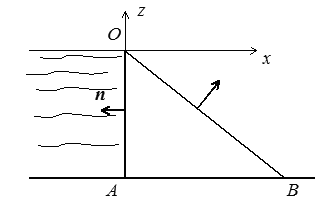Le barrage OAB (supposé dans la figure ci-contre triangulaire, mais cela n'a guère d'importance pour ce que nous faisons actuellement) est soumis sur sa paroi verticale OA à la pression de l'eau p = − ρo g z (remarquons au passage que, en écrivant cela nous avons déjà implicitement posée nulle la pression atmosphérique). On écrira donc
T = − p n = + ρo g z n
La paroi OB au contraire est − au sens où nous l'avons défini plus haut − une surface libre
T = 0
On serait par contre beaucoup plus démuni pour écrire les conditions de contact avec le sol. Certes il serait toujours possible de reprendre la discussion du paragraphe précédent et constater que, parmi les trois conditions de contact discutées plus haut, seul le contact adhérent peut être envisagé (pourquoi ?)Parmi ces trois conditions, seule la condition d'adhérence permet la réaction horizontale nécessaire pour équilibrer la pression de l'eau. (Imaginez-vous, indépendamment des problèmes d'étanchéité bien sûr, un barrage posé sur roulettes
Plus généralement, n'oublions pas que les équations différentielles d'équilibre assurent l'équilibre global. Cet équilibre global ne rajoute donc rien de nouveau, mais il peut être utile de le garder présent à l'esprit. Mais cela n'a guère de sens par rapport au problème physique. Une formulation correcte serait de considérer l'ensemble barrage + sol, et d'imposer à l'infini (ou suffisamment loin) des conditions de déplacements nuls, mais l'on augmente ainsi considérablement la taille du problème.
Problème régulier
Nous pouvons maintenant prendre un peu de recul. Une première règle s'impose
Les conditions aux limites portent sur le vecteur contrainte ou sur le vecteur déplacement,
jamais sur le tenseur des contraintes ou sur le tenseur des déformations (attention, c'est là la principale source d'erreur lorsque l'on commence la Mécanique des Milieux Continus). Bien évidemment les conditions aux limites en contraintes (sur le vecteur donc) seront ensuite, pour être utilisées, transférées sur le tenseur par la relation T = σ n, mais la condition elle-même porte bien sur les efforts appliqués à la structure, et donc sur le vecteur contrainte.
Si l'on examine plus en détail les divers exemples présentés plus haut, on constate que les conditions aux limites peuvent imposer
- les 3 composantes du vecteur contrainte ; c'est le cas le plus fréquent, elles sont d'ailleurs imposées nulles pour une surface libre ;
- les 3 composantes du vecteur déplacement ;
- une combinaison de ces conditions, comme par exemple le cas du contact sans frottement qui impose la composante verticale du déplacement et les composantes horizontales du vecteur contrainte.
Définition. Problème régulier.
Un problème régulier est un problème pour lequel les conditions aux limites imposent, en chaque point de la frontière et pour chacune des composantes, une valeur donnée au déplacement OU à la contrainte.
On écrira donc les conditions aux limites d'un problème régulier sous la forme
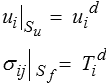
où uid et Tid sont les valeurs imposées, donc données du problème, c'est la signification de l'indice supérieur d,
et où Su et Sf sont les parties de la frontière S où sont respectivement imposés les déplacements et les contraintes.
On remarquera que cette écriture est en fait allégée, car les surfaces Su et Sf peuvent en fait dépendre de la composante. Il pourra même arriver que les repères par rapport auxquels sont prises ces composantes, diffèrent d'une surface à l'autre (cas d'un bloc pesant posé entre deux plans obliques avec un contact sans frottement).
Peu importe, cela ne pose aucun problème, sinon d'écriture. Nous nous limiterons donc à cette écriture parfois symbolique. L'essentiel est bien que l'on ait en chaque point trois conditions complémentaires. On regroupera alors sur Su toutes les conditions en déplacements et sur Sf toutes les conditions en contraintes.
Nous nous limiterons dans la suite aux problèmes réguliers qui assurent une formulation saine, et conduisent en général à un problème bien posé (c'est-à-dire admettant une solution unique). Ceci exclut nombre de conditions aux limites parfois utiles : contact avec frottement évoqué plus haut, contact unilatéral avec possibilité de décollement, appui élastique, etc..., mais ceci conduit à des problèmes mathématiques beaucoup plus difficiles.
Insistons à nouveau sur la nécessité de bien avoir, en chaque point de la surface, ces 3 informations (2 dans le cas bidimensionnel). S'il en manque, on perd l'unicité, et plusieurs solutions peuvent exister. Si l'on en a trop, on perd l'existence, et il peut ne plus exister de solution.
A nouveau le choix des conditions aux limites est une étape importante et souvent difficile dans la modélisation d'un problème physique.
Conditions de transmission
Nous avons déjà rencontré dans le cas du barrage un problème où intervenaient deux milieux différents (le barrage et le sol). C'est en fait une situation fréquente, notamment dans les matériaux ou structures composites. Il faut alors préciser les conditions de raccord.
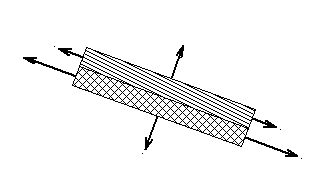Nous nous limiterons au cas de matériaux collés. La condition d'adhérence impose alors la continuité du vecteur déplacement à l'interface, tandis que l'équilibre impose la continuité du vecteur contrainte à l'interface : il suffit pour s'en convaincre d'écrire l'équilibre d'un disque mince coupant l'interface.
Les contraintes sur les facettes perpendiculaires à l'interface peuvent, elles, être discontinues, car elles s'équilibrent directement, comme le montre la figure ci-contre limitée aux contraintes normales. C'est une situation très courante dans les matériaux composites.
Conditions de transmission.
Entre deux matériaux a et b
uia = uib σija nj = σijb nj
où n est la normale à l'interface.
Ces conditions étendent au cas des structures composites la notion de problème régulier.