Théorème de l'énergie potentielle
Nous nous limitons désormais au cas de l'élasticité linéaire (<). La loi de comportement s'écrira donc
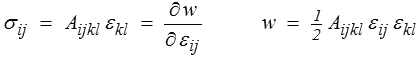
Energie potentielle d'un CCA
A tout CCA 
(x) (<) on associe son énergie potentielle U ( ) , quantité scalaire définie par
Définition.
L'énergie potentielle du CCA est la différence entre son énergie élastique et le travail des efforts donnés
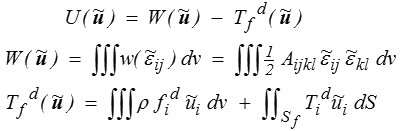
Enoncé du théorème
Le champ de déplacement solution d'un problème régulier est bien évidemment CCA, nous le noterons u ( x ) (sans tilde). Le théorème de l'énergie potentielle permet de le reconnaître dans cet ensemble.
Théorème de l'énergie potentielle.
Parmi tous les CCA ( x ) le champ solution minimise l'énergie potentielle
U ( u ) ≤ U ( )
Quelques commentaires
Ce théorème est suffisamment important et nouveau pour que, avant de le démontrer et de l'utiliser, nous prenions le temps d'en discuter la portée et la signification.
Le point le plus remarquable est que ce théorème change complètement la nature du problème, transformant un problème d'équations aux dérivées partielles en une simple recherche de minimum. C'est là quelque chose de tout à fait nouveau. Vraiment nouveau ?
Non, pas tout à fait, le lecteur vigilant se souvient peut-être du principe de moindre action (<) qui nous avait permis d'obtenir à partir d'un principe d'extremum les équations du mouvement sous la forme des équations de Lagrange. Ce type de méthode, basé sur le calcul des variations, est courant en mathématiques ; on parle de « méthodes variationnelles », ce qui explique le titre de ce chapitre.
Nous avons déjà discuté (<) un schéma de solution à partir d'un champ de déplacement postulé. Les étapes 1 et 2 correspondent à la construction d'un CCA. Les conditions 3 à 6 définissent les conditions supplémentaires que doit vérifier ce CCA pour être solution, et on peut maintenant leur substituer une recherche de minimum.
Il en résulte également que, une fois construit ce CCA, et même si l'on ne peut pas aller jusqu'au bout de la démarche et ainsi trouver la solution, on peut néanmoins en tirer une information exacte sur la solution, à savoir une borne supérieure de son énergie potentielle. Reste à savoir ce qu'elle représente. Patience ! cela viendra en son temps (>).
Un autre aspect important est le fait que ce théorème est la version « élastique » du principe universel de la physique affirmant que la solution d'un problème minimise l'énergie du système. Avec toutefois deux nuances essentielles
- Ici c'est un théorème, non un principe abstrait et parfois ambigu.
- Nous aurions été bien incapable de postuler a priori la forme de cette « énergie ».
Démonstration - Premier volet
La démonstration de ce théorème est, comme on peut s'en douter, un peu technique, et il est bien plus important de comprendre la signification et l'application de ce théorème que sa démonstration. Le lecteur pourra donc la sauter sans scrupule ou état d'âme. J'ai toutefois jugé utile de la donner car elle est instructive, et aussi pour vous montrer que, contrairement à d'autres résultats mathématiques que je cite sans démonstration, elle est tout à fait à votre portée.
Pour démontrer ce théorème nous allons comparer l'énergie potentielle d'un CCA (x) à celle de la solution (que l'on suppose exister, nous y reviendrons un peu plus loin). Nous posons donc
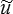i (x) =ui 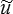(x) + io(x)
où o(x) est tel que
o(x)|Su = 0
C'est donc un CCA pour le « problème régulier homogène » (c'est-à-dire avec des données f d, T d et u d nulles) associé. On dira que o(x) est un CCAo. En termes géomètriques, l'espace des CCA est un espace affine d'espace vectoriel sous-jacent l'espace des CCAo.
L'énergie potentielle du CCA est alors
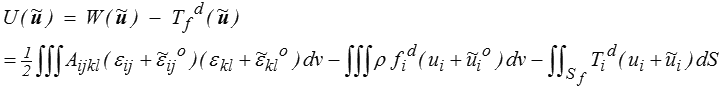
soit, en développant,
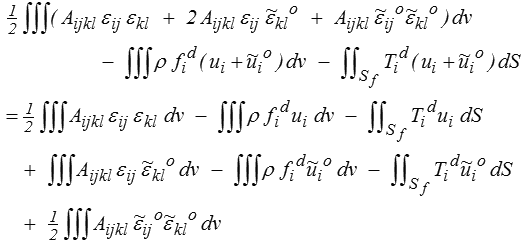
On reconnaît dans la première ligne du second membre l'énergie potentielle de la solution, et dans la dernière l'énergie élastique − toujours positive − associée à o. On peut donc écrire, en remarquant que la contrainte solution est
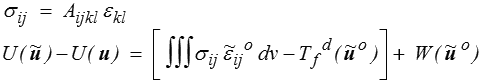
Nous nous intéressons désormais au terme entre crochets, linéaire en o : s'il est nul, alors
U ( ) − U (u) = W ( o) ≥ 0
et la solution u minimise l'énergie potentielle. Or, il est nul :
Lemme.
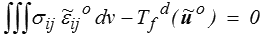
Pour démontrer ce lemme, nous considérons le problème régulier défini par les forces de volumes fi d et les conditions aux limites
σij nj|Sf = Tid ui|Su = 0
(Ce problème correspond aux efforts appliqués réels mais avec des déplacements donnés nuls). Le champ o est, par construction, CCA pour ce problème tandis que σij, champ de contrainte solution pour le problème réel, est CSA pour ce problème auxiliaire. Le lemme fondamental (<) donne alors
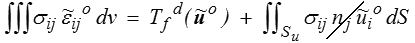
d'où la conclusion, puisque o est nul sur Su. Le lecteur effrayé par cette approche un peu alambiquée, ou méfiant et suspectant quelque entourloupe, pourra d'ailleurs vérifier directement ce résultat en intégrant par parties
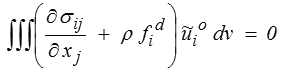
Démonstration - La réciproque
Pour qu'un CCA soit solution, il doit vérifier les conditions supplémentaires qui correspondent aux étapes 3 à 6 de la démarche de construction (<) d'une solution. Nous venons de montrer que si u vérifie ces conditions, il en résulte que l'énergie potentielle est minimum. Réciproquement nous voulons montrer que si l'on trouve un CCA minimisant l'énergie potentielle, cela suffit pour être certain que ces conditions supplémentaires − équations d'équilibre et conditions aux limites en efforts − sont vérifiées. C'est en fait cette réciproque qui fait la force du théorème de l'énergie potentielle et nous permet de changer radicalement la nature du problème
Nous partons donc d'un CCA u dont l'énergie potentielle est inférieure à celle de tout CCA. Il en résulte, d'après les calculs faits plus haut, que la quantité
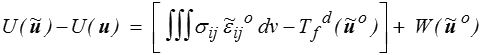
est positive pour tout CCAo o(x). On a noté σij le champ de contrainte associé à u , reste à montrer que ce σij est statiquement admissible.
Le terme entre crochets est linéaire en o, alors que le terme W ( o) est quadratique. On en tire par un raisonnement classique que ce terme entre crochets doit être nul. On peut, par exemple, remarquer que si o est CCAo alors λ o l'est aussi pour tout λ réel. On doit donc avoir
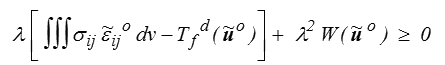
pour tout λ, ce qui exige d'une part que le terme en λ2 soit positif (il l'est puisque c'est une énergie) et d'autre part que le terme en λ soit nul. On a donc
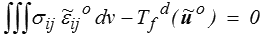
Nous allons maintenant faire une intégration par parties de l'intégrale de volume
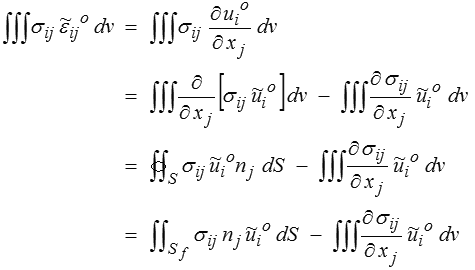
puisque o est nul sur Su. En regroupant avec les termes correspondants de Tfd il vient
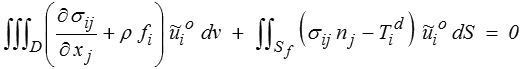
pour tout o soumis à la seule condition d'être nul sur Su. On en tire directement
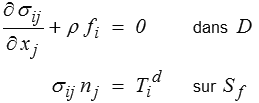
c'est-à-dire les équations statiques qui restaient à vérifier.
Théorème d'unicité
Nous avons affirmé qu'un problème régulier était, en élasticité linéaire, un problème bien posé, c'est-à-dire admettant une solution unique. Nous pouvons maintenant démontrer l'unicité de la solution.
Supposons en effet qu'il existe deux solutions u 1 et u 2 ; elles sont bien évidemment CCA. On peut écrire, en vertu des calculs précédents,
U ( u 1) = U ( u 2) + W ( u 1− u 2)
U ( u 2) = U ( u 1) + W ( u 2− u 1)
et donc
W ( u 1− u 2) = 0
L'énergie élastique étant définie positive (<) il en résulte
εij1− εij2 = 0 εij1= εij2
Les deux solutions correspondent à la même déformation, il y a unicité du champ de déformation, et donc aussi des contraintes.
Les deux déplacements u 1 et u 2 correspondant aux mêmes déformations ne peuvent différer que d'un mouvement de solide rigide. En général les conditions aux limites en déplacement imposeront ce mouvement de solide rigide, et il y aura aussi unicité du champ de déplacement. Ce ne sera toutefois pas toujours le cas, par exemple, si les conditions portent uniquement que les efforts, les déplacements ne seront alors définis qu'à un déplacement de solide rigide près.
Comme souvent en mécanique, le théorème d'unicité se démontre facilement ; il en va tout autrement du théorème d'existence, qui nécessite des outils mathématiques beaucoup plus sophistiqués.
Application
Considérons, à titre d'exemple ou d'exercice, notre problème modèle (<). Il est facile de construire un CCA. Nous pouvons par exemple prendre
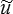1 = A x1 x2 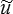2 =−B x1 x2
Le tenseur des déformations associé est (nous avons mis un signe moins pour 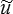2 car nous attendons un déplacement vers le bas : u2 ≥ 0 )
ε11 = A x2 ε22 =−B x1 ε12 = ½( A x1 − B x2 )
La loi de Hooke permettrait alors d'obtenir les contraintes
σ11 = ( λ+2 μ ) A x2 − λ B x1
σ22 = λ A x2 + ( λ+2 μ ) B x1
σ12 = μ ( A x1 + B x2 )
mais les équations d'équilibre et les conditions aux limites statiques ne pourront pas être vérifiées, notre CCA n'est pas solution.
Faute de pouvoir trouver une solution, utilisons notre théorème. La densité d'énergie élastique est, avec les coefficients de Lamé λ et μ,
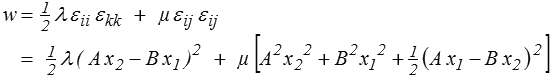
L'énergie de déformation W s'obtiendra ensuite par intégration (pour une tranche d'épaisseur unité)
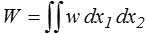
Après calcul (que je vous laisse le soin de détailler. Eh oui ! Il faut bien quand même faire parfois quelques calculs ; ce n'est pas très agréable, j'en suis bien d'accord, mais quand il faut !)
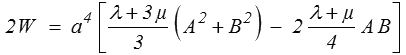
Le travail des efforts donnés s'obtient plus facilement ( x2 = a sur BC )
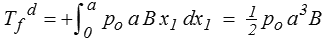
Le théorème de l'énergie potentielle s'écrit donc
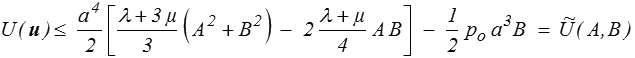
ce qui nous donne une borne supérieure de l'énergie potentielle de la solution, résultat incontestable mais de portée encore limitée.
Cela devient déjà plus intéressant si l'on remarque que ce résultat étant vrai pour toutes les valeurs des deux constantes A et B, il est judicieux de choisir ces valeurs pour rendre minimum la borne supérieure. Nous sommes donc amenés à écrire
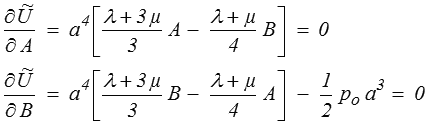
On trouve finalement, après quelques calculs (que vous pouvez refaire si le coeur vous en dit, mais qui n'apportent rien d'essentiel ; ici je vous suggère plutôt de garder pour plus tard vos envies de calcul) et en prenant pour fixer les idées λ = μ, c'est-à-dire (<) un coefficient de Poisson égal à 1/4,
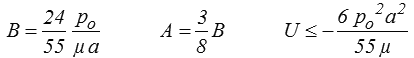
On pourra (légitimement) s'étonner de trouver une « énergie » (potentielle) négative. Nous reviendrons plus tard sur ce signe moins. Nous pouvons toutefois remarquer que le déplacement nul, u = 0, est un CCA d'énergie potentielle nulle. Le minimum de cette énergie potentielle est donc négatif.