Le bloc pesant
Formulation du problème
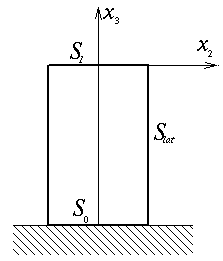Revenons au bloc pesant présenté (<) lorsque nous avons introduit les conditions aux limites d'un problème régulier. Nous considérerons donc un bloc cylindrique de base par exemple circulaire (en fait sa forme n'a aucune importance et nous pouvons travailler en coordonnées cartésiennes). Pour la commodité du calcul nous prenons l'origine sur la face supérieure.
Nous devons donc vérifier en tout point
- la loi de Hooke,
- les équations d'équilibre avec f = ( 0, 0, − ρ g )
- les conditions aux limites de bord libre sur la face supérieure et la surface latérale
S1 et Slat T = 0 - les conditions sur la face inférieure, qui sont plus complexes, où nous avions introduit trois modélisations :
- contact adhérent u = 0
- contact sans frottement u3 = 0 T1 = T2 = 0
- enveloppe souple T3 = + Pf T1 = T2 = 0
Champ de contrainte
Les conditions aux limites sur la surface latérale s'écrivent
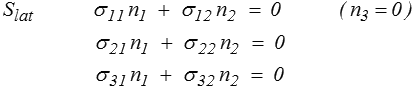
(avec par exemple pour une base circulaire n1 = cos θ , n2 = sin θ ). On remarque que ces conditions aux limites doivent être vérifiées en tout point de la surface, donc pour tout x3 et toute normale ( n1 , n2 , n3=0 ). Il serait tentant d'en déduire que puisque n1 et n2 peuvent être choisis quelconques
σ11 = σ12 = σ22 = σ31 = σ23 = 0
Cela n'est évidemment pas légitime. Pourquoi ?
Pour deux raisons. Tout d'abord les contraintes peuvent parfaitement dépendre de n, c'est-à-dire de l'orientation. D'autre part quand bien même ces contraintes seraient nulles sur le bord, elles n'ont aucune raison de le rester à l'intérieur. En fait l'argumentation suppose implicitement que les contraintes sont uniformes dans chaque section x3 = Cte.
Pour le problème de révolution, par exemple, ces conditions exigent simplement
σrr = σrθ = σrz = 0 pour r = a
La solution générale serait à chercher sous la forme
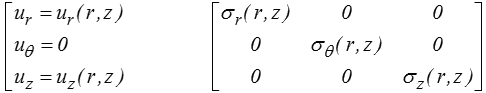
avec σr ( r = a , z ) = 0 pour tout z.
Nous ne pouvons donc pas conclure ainsi. Toutefois, rien n'interdit d'essayer. A nouveau, à partir du moment où nous savons qu'il existe une solution et qu'elle est unique, tous les moyens sont bons pour essayer de la trouver. Nous chercherons donc un champ de contrainte vérifiant ces conditions et donc avec une seule contrainte non nulle σ = σ33 , cette fonction pouvant éventuellement dépendre de x1 , x2 et x3.
Les équations d'équilibre donnent alors simplement
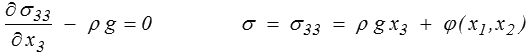
Mais la condition de surface libre sur la face supérieure donne
x3 = 0 σ13 = σ23 = σ33 = 0
la contrainte σ est donc nulle pour x3 = 0
σ = ρ g x3
et le champ de contrainte est complètement déterminé.
Contact par enveloppe souple
Dans le cas c. (contact par enveloppe souple) les conditions aux limites sur la base So s'écrivent ( n = − e3 ) :
x3 = −h σ33 = − Pf σ13 = σ23 = 0
Elles sont donc également vérifiées avec une pression de fluide
Pf = + ρ g h
(Nous aurions d'ailleurs pu trouver directement cette relation en écrivant que la réaction de pression Pf S doit équilibrer le poids du bloc ρ g S h ).
Avons-nous terminé ? Pas encore tout à fait : il faut encore calculer le déplacement ou tout au moins être certain de pouvoir le faire, c'est-à-dire vérifier les équations de Beltrami.
Ici, elles le sont, car le champ de contrainte est linéaire et les forces de volume sont uniformes. Les équations de Beltrami (<) sont donc vérifiées. Nous pouvons donc affirmer avoir trouvé la solution unique du problème du bloc pesant pour un contact par enveloppe souple. Bien entendu, il resterait à calculer le champ de déplacement, mais, est-ce indispensable ?
Calcul du déplacement
Ce calcul du déplacement est donc facultatif pour le problème c. ; il serait par contre obligatoire pour les deux problèmes a. et b., car les conditions aux limites sur So font intervenir ces déplacements.
Beltrami nous ayant rassuré sur la possibilité de mener ce calcul au bout, reste à le faire. La loi de Hooke donne directement
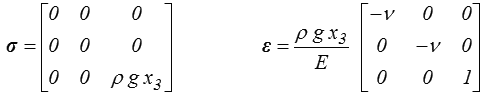
Les équations différentielles pour les déplacements sont donc, en posant α = ρ g / E
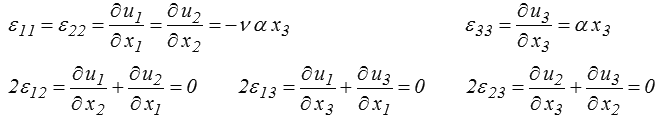
Le calcul est analogue à celui fait dans le cas de la flexion. Les trois premières équations s'intègrent directement pour donner
u3 = ½ α x32 + φ3 ( x1 , x2 )
u1 = − ν α x1 x3 + φ1 ( x2 , x3 )
u2 = − ν α x2 x3 + φ2 ( x1 , x3 )
et les trois suivantes se ramènent à
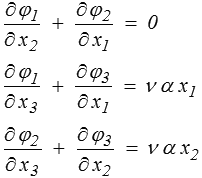
dont une solution particulière est
φ1 = φ2 = 0 φ3 = ½ ν α ( x12 + x22 )
On obtient donc, à un déplacement de solide rigide près (et en fixant u3 = 0 en x1 = x2 = 0 x3 = −h )
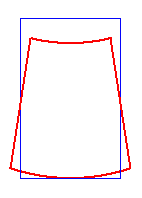
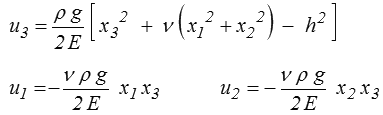
La déformée correspondante est représentée ci-contre.
Contact direct
Nous constatons donc que notre tentative a échoué pour les deux problèmes de contact direct (adhérent ou sans frottement) puisque la condition u3 = 0 ne peut pas être vérifiée, sauf dans le cas très particulier d'un coefficient de Poisson nul ( ν =0 ).
Que faire pour aller plus loin ? Pas grand chose pour l'instant d'un point de vue théorique. D'un point de vue pratique, on peut toutefois utiliser cette solution comme une approximation de la solution du problème réel, qui de toute façon avait déjà dû être fortement idéalisée pour mener à un problème régulier. Le choix des conditions aux limites pour permettre ou faciliter l'obtention d'une solution approchée participe à l'art de l'Ingénieur.