Le cadre variationnel
Statique et cinématique
L'ensemble des résultats obtenus jusqu'à présent peut se schématiser en un diagramme rectangulaire

Lu par colonne, ce schéma résume la description
du mouvement (colonne de droite, cinématique).
Le vecteur déplacement u(x) permet de calculer le tenseur des déformations ε par les relations (<)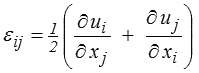
des efforts (colonne de gauche, statique).
Les conditions aux limites (<)Ti = σij nj
et les équations d'équilibre (<)
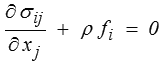
permettent d'exprimer, en fonction des contraintes, les efforts volumiques ρf et le vecteur contrainte T (efforts surfaciques).
Initialement formulée dans le cas statique ou quasi-statique (<) cette schématisation peut s'étendre au cas dynamique en rajoutant aux forces de volume les forces d'inertie, on parle souvent alors d'équilibre dynamique.
Structure et matériau
Lu par lignes on distingue
- la structure (étage supérieur) : c'est l'objet physique réel sur lequel on peut appliquer ou mesurer des efforts et observer ou imposer des déplacements.
- le matériau (étage inférieur), concept abstrait mais qui permet d'introduire, au travers de la loi de comportement, les caractéristiques physiques de la matière constituant cet objet.
Pour déterminer la réponse de notre objet structure, c'est-à-dire relier son mouvement aux efforts qui lui sont appliqués, il faut passer par l'étage souterrain du matériau. Là est toute la problématique du calcul des structures.
Nous avons déjà rencontré cette problématique lorsque nous avons discuté les lois de comportement (<) : nous avons en effet insisté sur le fait que le matériau ne pouvait être caractérisé qu'au travers d'une structure judicieusement choisie (les essais mécaniques).
C'est ce concept de matériau qui en fait permet d'appliquer à telle ou telle structure réelle (tuyauterie, navire, machine,...) les résultats obtenus dans un essai de traction. Remarquons incidemment que cette extrapolation n'est pas sans risque et que, pour certains types de problèmes, la réponse peut significativement dépendre de la taille de la structure considérée. On parle souvent d'« effet d'échelle », et nous nous bornerons pour l'instant à constater que ces effets sont − par essence − exclus du cadre de la MMC telle que nous la développons dans ce cours.
Calcul des structures
Cette construction algébrique est en fait tout à fait générale, et on la retrouvera dans tout modèle de structure. Nous l'avons ici introduite dans le cadre de la MMC bi- ou tridimensionnelle, mais on la retrouvera lorsqu'on cherchera à développer d'autres modélisations (théorie des poutres, plaques,...).
En fait, la première étape dans le développement d'un nouveau modèle sera la reconstruction de ce diagramme rectangulaire

Une fois construit ce diagramme, tous les résultats, théorèmes et méthodes que nous développerons dans ce chapitre, pourront immédiatement s'appliquer.
On remarquera également que le théorème des travaux virtuels affirme l'égalité des travaux virtuels des efforts intérieurs et extérieurs, donc en termes mathématiques de deux produits de dualité < statique, cinématique > à l'échelle de la structure et à l'échelle du matériau. Il en résulte que l'opérateur donnant les efforts extérieurs en fonction des contraintes est l'adjoint ou dual de celui donnant les déformations en fonction du déplacement. C'est, sans jeu de mot, la structure de base pour une formulation générique de la Mécanique des Structures.
CCA et CSA
Pour résoudre un problème de MMC il faut donc trouver le déplacement ui (x) et les contraintes σij (x). On notera la dissymétrie entre ces inconnues de base : variable cinématique à l'étage structure, variable statique à l'étage matériau. Le schéma précédent permet en effet de déterminer les variables correspondantes à l'autre étage : déformations et efforts extérieurs. Outre les « équations du champ » qui doivent être vérifiées en tout point, ces deux champs doivent vérifier les conditions aux limites.
Nous avons discuté plus haut les conditions aux limites (<), et en nous limitant aux seuls problèmes réguliers ces conditions portent soit sur le déplacement (conditions cinématiques) soit sur les efforts (conditions statiques).
Nous pouvons introduire
Définition.
Un champ cinématiquement admissible (CCA) est un champ de déplacement 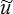 i (x) vérifiant toutes les conditions cinématiques
i (x) vérifiant toutes les conditions cinématiques
soit en fait en MMC les conditions aux limites de type cinématique
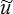 i |Su = uid
i |Su = uid
Mais plus généralement, des équations de champ pourront également s'imposer, par exemple pour un matériau incompressible l'équation div 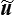 = 0 traduisant l'incompressibilité. De même, pour une structure composite, il faudra également vérifier les conditions de transmission cinématiques à l'interface entre deux matériaux a et b (<)
= 0 traduisant l'incompressibilité. De même, pour une structure composite, il faudra également vérifier les conditions de transmission cinématiques à l'interface entre deux matériaux a et b (<)
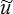 ia =
ia = 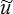 ib
ib
Définition.
Un champ statiquement admissible (CSA) est un champ de contrainte  ij (x) vérifiant toutes les conditions statiques
ij (x) vérifiant toutes les conditions statiques
c'est-à-dire les équations d'équilibre
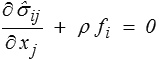
et les conditions aux limites statiques
 ij nj |Sf = Tid
ij nj |Sf = Tid
sans oublier d'éventuelles conditions de transmission (<)
 ija nj =
ija nj =  ijb nj
ijb nj
Avec ces deux définitions la formulation d'un problème régulier devient
La solution d'un problème régulier est l'ensemble d'un CCA ui(x) et d'un CSA σij(x) reliés par la loi de comportement.
Le lemme fondamental
Toutes les démonstrations qui suivent s'appuieront essentiellement sur
Lemme fondamental.
Pour tout CCA 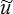 i et tout CSA
i et tout CSA  ij
ij
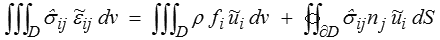
Ce lemme est très proche du théorème des travaux virtuels (<) qu'il étend très légèrement au cas d'un champ de contrainte statiquement admissible (au lieu de la solution). Cette extension est toutefois directe car la démonstration ne faisait intervenir que les équations d'équilibre (rappelons que nous nous sommes limités au cas quasi-statique). Par contre, ce lemme particularise le théorème des travaux virtuels en le limitant aux CCA qui sont des déplacements virtuels très particuliers. On peut alors réécrire le second membre
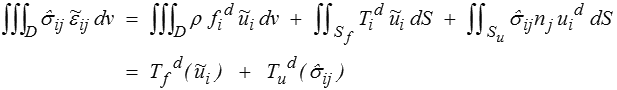
en introduisant
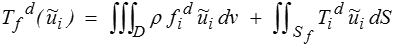
travail des efforts donnés dans le déplacement 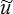 i et
i et
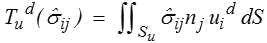
travail du CSA  ij dans les déplacements donnés.
ij dans les déplacements donnés.
Conformément à nos conventions de notations, nous avons rajouté un indice supérieur « d » aux forces de volume pour rappeler que ce sont aussi des efforts donnés et connus.
Un exemple
Nous illustrerons ce chapitre au travers d'un exemple simple que nous suivrons tout au long de sa progression.
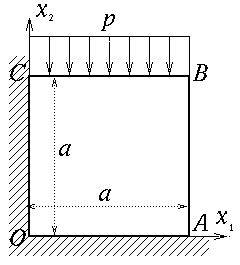 Nous considérons les déformations planes (u3 = 0) d'un carré OABC de côté a. Ce solide est fixé sur ses deux faces OA et OC et soumis sur sa face supérieure BC à l'action d'une pression verticale po, tandis que sa face latérale AB est libre.
Nous considérons les déformations planes (u3 = 0) d'un carré OABC de côté a. Ce solide est fixé sur ses deux faces OA et OC et soumis sur sa face supérieure BC à l'action d'une pression verticale po, tandis que sa face latérale AB est libre.
Vous pouvez donc écrire les conditions aux limites. (Exercice)
face OC ( x1 = 0 ) u1 = u2 = 0
face OA ( x2 = 0 ) u1 = u2 = 0
face AB ( x1 = a ) σ11 = σ12 = 0
face BC ( x2 = a ) σ12 = 0 , σ22 =−po
Ce problème n'admet pas de solution simple. (Si vous n'en êtes guère persuadé quelques essais malheureux auront vite fait de vous convaincre).
Un CCA sera un champ 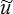 i tel que
i tel que
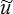 i = 0 pour x1 = 0 et pour x2 = 0
i = 0 pour x1 = 0 et pour x2 = 0
tandis qu'un CSA sera un champ de contrainte  11 (x),
11 (x),  12 (x),
12 (x),  22 (x) vérifiant les équations d'équilibre
22 (x) vérifiant les équations d'équilibre
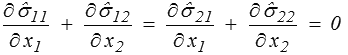
et les conditions aux limites
en x1 = a  11 =
11 =  12 = 0
12 = 0
en x2 = a  12 = 0 ,
12 = 0 ,  22 =−po
22 =−po
Le lemme fondamental devient
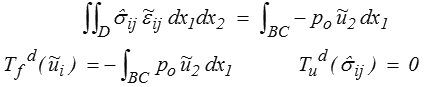
en remarquant que la seule donnée non nulle est la pression po imposée sur la face supérieure (on néglige les forces de volume).
