Puissances et travaux virtuels
Le point matériel
La notion de puissance et de travail est une notion essentielle en physique et qui renvoie classiquement sur la notion d'énergie et donc, pourrait-on croire, vers la thermodynamique. Nous y viendrons effectivement plus loin, mais cela n'est pas encore à l'ordre du jour.
En mécanique le travail d'une force s'obtient en faisant le produit d'une force par le déplacement de son point d'application (produit scalaire, si l'on s'intéresse aussi à leur direction). Il s'exprime en joules
1 J = 1 Nm = 1 kg m2s−2
De même la puissance est le travail par unité de temps, donc le produit (scalaire) de la force par la vitesse et s'exprime en watts
1 W = 1 J/s = 1 kg m2s−3
En mécanique du point matériel cette notion s'introduit tout naturellement en faisant le produit scalaire de l'équation du mouvement (<) par la vitesse
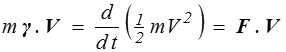
C'est le théorème de l'énergie cinétique pour un point matériel soumis à une force F.
La dérivée par rapport au temps de l'énergie cinétique est égale à la puissance de la force appliquée.
ou si l'on préfère :
Le travail de la force est égal à la variation de l'énergie cinétique. En d'autres termes le point stocke sous forme d'énergie cinétique (½ mV 2 ) le travail qui lui est fourni. Le théorème de l'énergie cinétique est un bilan d'énergie mécanique et c'est une conséquence de la loi du mouvement.
Mouvements virtuels
Survient alors un mathématicien qui nous fait remarquer que, plutôt que d'écrire l'équation vectorielle du mouvement, il revient au même d'en faire le produit scalaire par un vecteur quelconque
m γ . φ = F . φ pour tout vecteur φ.
C'est ce que le mathématicien appelle une formulation « faible », par opposition à la formulation « forte » qu'est l'équation vectorielle (pourquoi « faible » et « forte » ? ce n'est pour l'instant qu'un tic de langage, ces deux formulations sont bien évidemment équivalentes ici; la distinction prendra par contre tout son sens plus tard). Si d'aventure il me plaît d'interpréter φ comme une vitesse V*, alors il vient
m γ . V* = F . V*
Le vecteur V* est quelconque et donc sans rapport avec le mouvement réel – le terme « mouvement virtuel » souligne ce caractère arbitraire −. On obtient donc le
Théorème des puissances virtuelles pour un point matériel.
Pour tout mouvement virtuel la puissance virtuelle de la quantité d'accélération est égale à la puissance virtuelle de la force appliquée.
(On ne peut bien évidemment plus parler d'énergie cinétique.)
Puisque nous avons choisi comme point de départ l'équation du mouvement, il s'agit là d'un théorème. Il serait par contre tout à fait légitime de prendre cet énoncé comme point de départ. On parlera alors de « principe des puissances virtuelles », et l'équation du mouvement deviendra alors un théorème. Cette approche alternative est tout à fait digne d'intérêt et elle conduit à des démarches souvent élégantes et parfois très efficaces mais, dans ce cours, nous ne l'évoquerons qu'à la marge.
Le théorème des puissances virtuelles
Pour un point matériel la situation est donc claire : la loi fondamentale F = m γ implique le théorème des puissances virtuelles, qui lui est en fait équivalent.
Ce résultat reste-t-il vrai pour un système mécanique quelconque ? La réponse est NON, tout au moins si l'on s'en tient à l'énoncé qui lui a été donné plus haut. Eh bien, qu'à cela ne tienne, nous allons modifier l'énoncé pour qu'il devienne vrai.
Théorème des puissances virtuelles.
La puissance virtuelle des quantités d'accélération est, pour tout mouvement virtuel, égale à la puissance virtuelle des efforts extérieurs et des efforts intérieurs
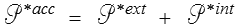
Mais que sont ces efforts intérieurs ? La Mécanique ne connaît en fait que les efforts extérieurs. Les efforts intérieurs sont une invention des mécaniciens qui, après avoir choisi un système, dénomment ainsi les efforts extérieurs − seuls porteurs de sens − exercés par une partie du système sur la partie complémentaire. C'est donc là une notion conventionnelle et très relative − quant à leur puissance !!
Dans certains cas, notamment pour un système de points matériels en interaction, on pourra la définir assez naturellement, mais ce ne sera en général pas le cas. Le théorème des puissances virtuelles est en fait la définition de la puissance des efforts intérieurs, et c'est bien comme cela que nous l'utiliserons dans la suite : la « puissance virtuelle des efforts intérieurs » est ce qu'il faut rajouter à la puissance virtuelle des efforts extérieurs (qui, elle, sera définie sans ambiguïté) pour rendre vrai le théorème des puissances virtuelles.
D'où un premier résultat : La puissance virtuelle des efforts intérieurs est nulle pour un point matériel. Beaucoup de bruit pour rien ? Pour l'instant certes, mais patience !
Le théorème des travaux virtuels
Tout ce qui précède est parti de notre interprétation du vecteur arbitraire φ (introduit par le mathématicien dans sa formulation faible) comme une vitesse. D'aucuns préfèrent l'interpréter comme un déplacement virtuel conduisant ainsi « mutis mutandi » au
Théorème des travaux virtuels.
Le travail virtuel des quantités d'accélération est, pour tout déplacement virtuel δu, égal au travail virtuel des efforts extérieurs et des efforts intérieurs
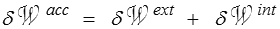
C'est ici le symbole δ qui, comme l'étoile pour les vitesses, rappelle le caractère virtuel, c'est-à-dire en fait arbitraire, du déplacement virtuel.
Puissances virtuelles ou travaux virtuels ? C'est une question de goût, de culture ou d'habitude.
