Quadriques des Contraintes
Détail de la construction
Le graphe ci-dessous est représenté pour
s2 = 1 , s1 = 1/4
La quadrique des contraintes est
- un ellipsoïde si les contraintes normales principales sont toutes de même signe,
- un hyperboloïde si elles sont de signes différents.
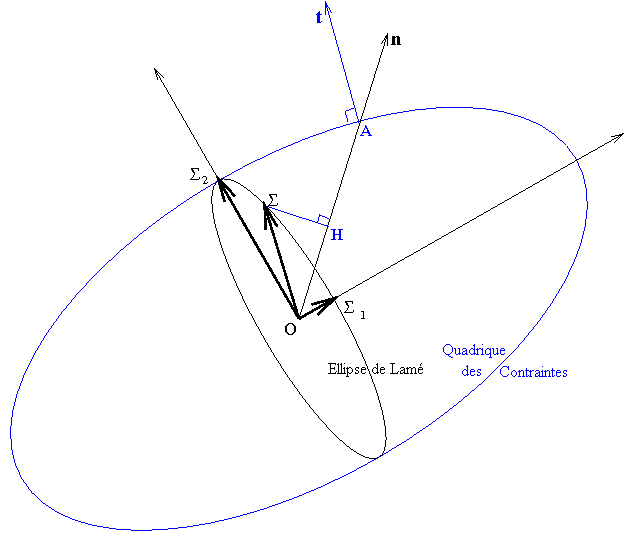
Pour déterminer le vecteur contrainte T = OΣ associé à une facette de normale n :
- On détermine l'intersection A de la quadrique des contraintes avec la demi-droite On de direction n.
- La direction du vecteur contrainte T = OΣ est donnée par la normale At à la quadrique des contraintes.
- Le point H, projection de Σ sur On, est donné par OH = 1/OA2.
(Le point Σ est évidemment sur l'ellipse de Lamé).
Animation
Une animation vous est proposée, permettant de visualiser, en fonction de l'état de contraintes bidimensionnel
- l'ellipse de lamé
- la quadrique des contraintes (ellipse ou hyperbole)
- l'évolution des points correspondants en suivant l'orientation de la facette
Vous pouvez télécharger cette animation réalisée en Java et vous trouverez ici comment l'utiliser
