Le solide rigide
Un solide rigide est un système mécanique indéformable c'est-à-dire dans lequel les longueurs et les angles entre points matériels ne changent pas au cours du temps.
Equiprojectivité
Théorème.
Une CNS pour que la distance entre deux points A et B ne change pas est que
[ V(A) − V(B) ] . AB = 0
La démonstration est directe : l'invariance de la distance s'écrit
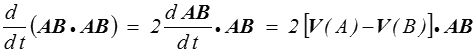
Un champ de vitesses, c'est-à-dire une vitesse définie en tout point x , sera dit équiprojectif s'il vérifie cette condition pour tout couple A , B.
On en déduit directement qu'une CNS pour qu'un système − continu ou discret − soit un solide rigide, c'est-à-dire sans variation de longueur, est que son champ des vitesses soit équiprojectif. Si maintenant l'on considère 3 points A, B et C, un calcul simple
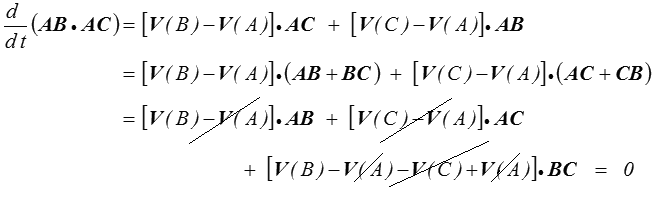
montre que le produit scalaire AB . AC = |AB| |AC| cos(AB, AC) reste également invariant et donc que les angles ne varient pas non plus. Les longueurs et les angles restent invariants dans un solide rigide.
Remarquons aussi que cette caractéristique introduite pour le champ de vitesses réelles (solide rigide) reste vraie pour un champ de vitesses virtuelles. On parlera alors d'un champ de vitesses rigidifiant, que l'on notera parfois
[ V R(A) − V R(B) ] . AB = 0
Distributeur des vitesses
Théorème.
Une CNS pour qu'un champ de vitesses soit équiprojectif est qu'il soit le champ des moments d'un « torseur distributeur » des vitesses
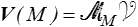
En d'autres termes, il existe un vecteur Ω , dit vecteur rotation, tel que
V(B) = V(A) + Ω ∧ AB
formule fondamentale de la cinématique du solide, qui n'est rien d'autre que la formule de transport des moments pour un torseur (<) que nous appellerons torseur distributeur des vitesses (<) et que nous noterons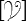 
avec
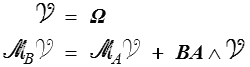
La condition suffisante est directe :
[ V(A) − V(B) ] . AB = (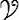 
∧ AB ) . AB
La démonstration de la condition nécessaire est technique et plus laborieuse. Nous renvoyons le lecteur à la littérature.
Puissance d'un système de forces
Si l'on considère un système de forces Fi exercées en Mi (système discret ou continu, peu importe ; dans ce dernier cas il suffirait de remplacer les sommes finies par des intégrales), sa puissance dans un champ de vitesses rigidifiant réelles ou virtuelles sera
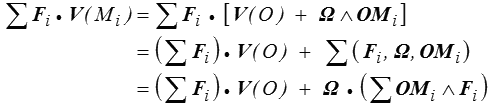
d'après les propriétés du produit mixte. La puissance s'écrit donc finalement, en notant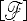 
le torseur des efforts Fi,
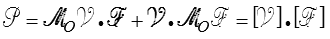
en introduisant le produit scalaire (<) des deux torseurs 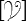et .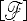
L'aspect essentiel de ce résultat est que, dans un mouvement rigidifiant, la puissance d'un système de forces ne dépend que de leur torseur.
Puissance des efforts intérieurs
On obtient en corollaire un résultat fondamental.
Théorème.
La puissance virtuelle des efforts intérieurs est nulle dans tout mouvement rigidifiant.
En effet, un champ de vitesses rigidifiant est défini par son torseur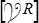 
. Le produit scalaire de la loi fondamentale par ce torseur donne
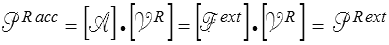
où l'indice supérieur R indique un champ de vitesses virtuelles rigidifiant.
Dans tout mouvement virtuel rigidifiant la puissance des quantités d'accélération est égale à la puissance des efforts extérieurs. La puissance des efforts intérieurs est donc nulle, d'après le théorème des puissances virtuelles (<)
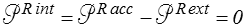
Nous avons déjà insisté sur le caractère conventionnel et relatif de la notion d'efforts intérieurs et donc a fortiori de leur puissance. Comme nous l'avons dit plus haut le « théorème des puissances virtuelles » constitue en fait la « définition » de la puissance des efforts intérieurs.
Dans le cas d'un système de particules en interaction toutefois, nous avions défini sans ambiguïté les efforts intérieurs et leur puissance. On peut alors vérifier directement ce théorème en partant de l'expression trouvée alors pour la puissance des efforts intérieurs
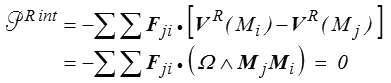
puisque par hypothèse Fji est colinéaire à Mi Mj.
C'est également ce théorème qui conduit, dans le bilan d'énergie associé au théorème de l'énergie cinétique, à interpréter la puissance des efforts intérieurs comme étant utilisée pour la déformation du système.
Mécanique du solide rigide
La position d'un solide rigide est, dans l'espace, définie par 6 paramètres : 3 paramètres de position et 3 paramètres d'orientation (par exemple, les 3 coordonnées du centre d'inertie et 3 angles d'Euler). La loi fondamentale donne, pour étudier le mouvement du système, 6 équations différentielles du second ordre. Elle suffit donc, complétée par des conditions initiales donnant à l'instant t = 0 position et vitesse, pour déterminer complètement le mouvement, si l'on connaît les efforts extérieurs. C'est la mécanique du solide rigide, pour laquelle on peut complètement oublier les efforts intérieurs, que l'on serait d'ailleurs bien en peine de définir précisément.
Ces efforts intérieurs réapparaîtront toutefois pour un système de plusieurs solides rigides, en tant qu'efforts de liaison entre solides. Il faudra alors écrire la loi fondamentale pour chacun des solides, caractériser les liaisons et leurs efforts pour finalement obtenir un système différentiel qui, par intégration, déterminera le mouvement. C'est ce que l'on appelle traditionellement la Mécanique Générale.
Dans le cas conservatif, c'est-à-dire dans le cas des liaisons parfaites, le formalisme hamiltonien et les équations de Lagrange (<) sont particulièrement recommandés, c'est la Mécanique Analytique.