Problèmes d'élasticité
Problèmes réguliers
Armés de la loi de Hooke, nous pouvons revenir à la formulation et à la résolution d'un problème. Nous nous limiterons désormais au cas quasi statique. La résolution d'un problème d'élasticité revient à trouver un champ de déplacement et un champ de contrainte vérifiant
- les équations d'équilibre,
- la loi de comportement,
- les conditions aux limites.
Pour un problème régulier, ces conditions aux limites doivent prescrire en tout point de la surface 3 composantes du vecteur contrainte ou du vecteur déplacement (<). Nous écrirons
ui|Su= uid σij nj|Sf = Tid
Problème régulier.
Trouver ui(x) et σij(x) vérifiant
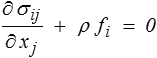
- la loi de Hooke
- ui|Su= uid σij nj|Sf = Tid
On démontre que, ainsi posé, un problème d'élasticité est « bien posé », c'est-à-dire qu'il admet une et une seule solution. Nous admettons pour l'instant ce théorème .
Ce théorème est essentiel car il nous garantit d'une part que, une fois formulé ainsi, il existe une solution, mais surtout d'autre part que, si nous arrivons à trouver une solution, ce sera la bonne !
Comment trouver cette solution ? Eh bien, malheureusement, en général on ne sait pas ! Plus exactement on ne sait résoudre explicitement que des problèmes très simples. Néanmoins ces solutions simples sont très utiles et permettent souvent de donner une première réponse. La démarche est en fait très empirique. Une fois garantie l'unicité de la solution, tous les moyens sont bons pour la trouver.
Une démarche saine est de commencer par établir une liste exhaustive des conditions qui doivent être vérifiées, puis de faire, à partir de notre intuition ou de l'expérience, des hypothèses sur le champ de contrainte et/ou de déplacement. On reporte alors dans les diverses équations qui doivent être vérifiées, précisant ainsi, au fur et à mesure, la solution.
- Si l'on arrive au bout de la démarche en vérifiant toutes les conditions, c'est gagné, on a trouvé la solution.
- Sinon, on met à la poubelle et on essaie autre chose. Gardons toutefois la poubelle à portée de main, elle pourra resservir (>).
Solutions homogènes
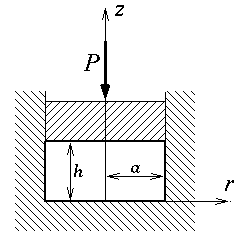Lors de la présentation des essais mécaniques, nous avons souligné l'intérêt des essais homogènes, qui permettent, sinon de mesurer, du moins de calculer les contraintes. Il est instructif de préciser les problèmes réguliers correspondants. Considérons par exemple l'essai oedométrique dans un moule. Il faut d'abord supposer que les contacts sont sans frottement. Il est alors facile d'écrire les conditions aux limites.
Nous supposons, pour fixer les idées, le moule circulaire de rayon r = a et nous utilisons les coordonnées cylindriques.
z = 0 (fond) uz = 0 Tr = Tθ = 0
r = a (parois latérales) ur = 0 Tz = Tθ = 0
z = h (face supérieure) uz = − U Tr = Tθ = 0
Nous avons ici supposé que le piston était rigide et imposait donc son déplacement vertical U.
Si nous complétons par les équations d'équilibre et la loi de Hooke, nous obtenons un problème régulier qui admet une solution unique, et c'est celle que nous avons donnée (<)
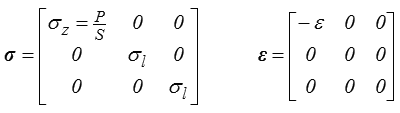
avec un champ de déplacement
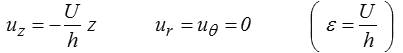
En effet, ce champ de déplacement engendre une contrainte homogène (les équations d'équilibre seront donc automatiquement vérifiées) donnée par la loi de Hooke
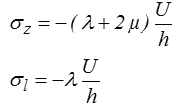
qui vérifie toutes les conditions aux limites. On obtient ainsi le rapport des contraintes σl / σz et la force P exercée
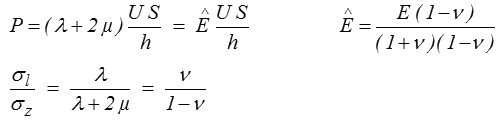
La mesure de P donnera donc le module oedométrique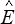 
et il faudrait, pour obtenir le coefficient de Poisson, mesurer la contrainte latérale σl .
On remarquera que dans cette formulation on impose le déplacement, et la force P est le résultat du calcul. Remarquons toutefois que l'on aurait tout aussi bien pu supposer que c'était la contrainte σz que l'on imposait égale à P / S, et remplacer la condition aux limites en z = h par
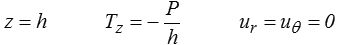
Ce sont des problèmes différents, qui se trouvent simplement avoir la même solution. Il serait par contre faux d'imposer à la fois uz = − U et Tz = − P / h.
En guise d'exercice, le lecteur pourra traiter de la même manière l'essai de compression plane (<), puis réfléchir sur l'essai de traction simple (attention, c'est plus difficile !).
Torsion et flexion
La torsion et la flexion, dont nous avons également abordé l'étude, correspondent à des solutions non homogènes.
Le problème de torsion (<) est relativement simple, puisque, pour construire le champ de déplacement, nous sommes partis de conditions aux limites en imposant à l'extrémité x1 = l une rotation Δ ø tout en maintenant fixe l'autre extrémité x1 = 0. Le problème aux limites est donc
So : x1 = 0 u1 = u2 = u3 = 0
S1 : x1 = l u1 = 0 u2 = − Δø x3 u3 = + Δø x2
Slat : r = a T = 0
et nous avons bien construit la solution unique de ce problème en prenant
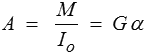
Attention toutefois, cette solution ne fonctionne que pour un arbre de section circulaire. Pour un arbre de section quelconque on trouvera la solution sans le polycopié (§VII-2 pp73-82, torsion de Saint-Venant)
Dans le cas de la flexion (<) nous avons bien trouvé une solution
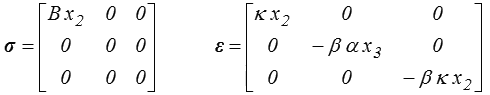
Nous avions, pour ce faire, pris une relation linéaire entre contrainte et déformation. C'est justement la loi de Hooke, en prenant simplement
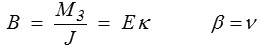
Quelles sont les conditions aux limites du problème que nous avons résolu ?
Sur la surface latérale, le vecteur contrainte est nul ; mais qu'obtient-on sur les sections d'extrémités ? Examinons par exemple la section x1 = l . Les vecteurs contrainte et déplacement y sont donnés par
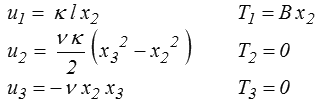
et l'on sait qu'il faut en chaque point et pour chaque composante imposer l'une de ces deux conditions.
- Pour la composante 1, il est plus facile d'imposer le déplacement u1 qui correspond simplement à une rotation κ l autour de x3 .
- Pour les deux autres composantes, on ne peut assurément pas imposer u2 et u3 , c'est donc T2 et T3 qu'il faut imposer nuls, mais il resterait à imaginer un mécanisme technologique permettant d'assurer ces deux conditions, tout en imposant un déplacement u1 linéaire en x2 , c'est-à-dire une rotation autour de x3 . Si B >0 alors pour x2 < 0 on est en compression ( T1 < 0 ), c'est simplement une condition de non frottement ; mais en traction (x2 > 0) voilà un joli défi technologique.
(On retrouverait d'ailleurs en fait le même problème en traction simple). C'est néanmoins la formulation correcte du problème de flexion
Slat (surface latérale) T = 0
x1 = 0 u1 = 0 T2 = T3 = 0
x1 = l u1 = κ l T2 = T3 = 0
que l'on sera bien incapable d'imposer réellement. C'est en fait le principe de Saint-Venant polycopié (§VII-1.1, p 67 ) qui, ici, nous sauvera ; sans lui nous avons bien trouvé une solution, mais pratiquement irréalisable.
Un schéma de résolution
Pour tenter de construire une solution, on pourra souvent partir d'une hypothèse sur le champ de déplacement (c'est à peu près ce que nous avons fait pour la torsion). Nous devons ensuite vérifier toutes les conditions, à savoir :
Problème d'élasticité.
| ui|Su= uid | CL cinématique |
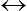σij  εij |
Loi de Hooke |
 |
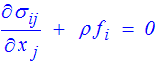Equations d'équilibre |
| σij nj|Sf = Tid | CL statique |
Nous avons ici réordonné et colorisé ces équations (en rouge et en haut, les conditions de type cinématique, en bleu et en bas les conditions de type statique. La loi de Hooke, elle, est en noir car elle n'est ni cinématique ni statique, mais assure le lien entre les deux aspects). Partant du champ de déplacement on peut directement vérifier les conditions aux limites cinématiques, tandis que les autres exigeront le calcul des contraintes. On arrive donc naturellement au schéma de résolution suivant :
Schéma 1.
- Faire une hypothèse sur le champ de déplacement.
- Vérifier les conditions aux limites cinématiques.
- Calculer les déformations εij .
- Calculer les contraintes σij (loi de Hooke).
- Ecrire les équations d'équilibre.
- Vérifier les conditions aux limites statiques.
Si l'on arrive au bout de ce programme, on aura trouvé la solution (et la solution sera alors complètement déterminée ; si tel n'est pas le cas, on se sera trompé quelque part : la solution est unique).
Sinon, tant pis, il faut essayer autre chose, et cet essai est à mettre (provisoirement) à la poubelle.
Outre la torsion déjà mentionnée, on utilisera notamment ce schéma de résolution pour
- le réservoir sphérique ===>,
- les enveloppes cylindriques.
Equations de Navier
Les étapes 3, 4 et 5 du schéma précédent reviennent en fait à substituer dans les équations d'équilibre l'expression des contraintes en fonction des déplacements
σij = λ εkk δij + 2 μ εij
= λ uk,k δij + μ (ui, j + uj,i )
J'utilise ici la notation classique de la dérivée partielle par une virgule :
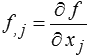
Donc
σij, j = λ uk,ki + μ ui, jj + μ uj, ji
= ( λ + μ ) uk,ki + μ ui, jj
Les équations du mouvement (car il ne coûte pas cher ici de rajouter le terme d'inertie et c'est, pour certains problèmes, très utile) s'écrivent donc en fonction des déplacements sous la forme
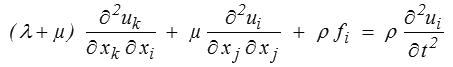
ce sont les équations de Navier. On les écrit souvent sous forme vectorielle
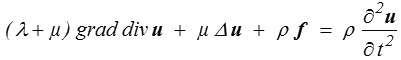
forme qui fait intervenir le laplacien Δ u d'un vecteur comme étant le vecteur dont, en repère cartésien, les composantes sont les laplaciens des composantes. Le calcul est donc facile en coordonnées cartésiennes. En coordonnées curvilignes (sphériques ou cylindriques notamment) ce sera plus compliqué et dans les formulaires élémentaires on ne trouvera pas toujours son expression. On utilise plutôt la forme équivalente
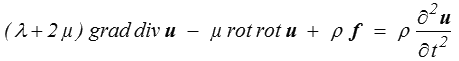
Ces équations permettent (dans le schéma de résolution précédent) de regrouper les étapes 3, 4 et 5, ce qui peut parfois être commode. Elles ne contiennent toutefois aucune information nouvelle, et il faudra de toute façon calculer les contraintes ; le bénéfice n'est pas si grand.
Mentionnons également l'équation de la dilatation, obtenue en prenant la divergence de l'équation précédente
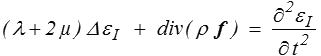
où εI = div u représente la dilatation, variation relative de volume. En particulier, en quasi statique et si les forces de volume sont nulles ou constantes, la dilatation est une fonction harmonique.
Autre schéma de résolution
Dans d'autres problèmes, et en fonction de notre inspiration, il pourra être plus commode de partir des contraintes. La démarche sera analogue, mais en remontant la pile des équations que nous avions parcourue dans le sens descendant. Une difficulté supplémentaire apparaît alors lorsque, après avoir vérifié les conditions statiques, on veut passer à la cinématique : la loi de Hooke donne les déformations, mais on se souvient que pour pouvoir remonter des déformations aux déplacements il faut satisfaire aux équations de compatibilité (<). Le schéma de résolution devient alors :
Schéma 2.
- Faire une hypothèse sur le champ des contraintes.
- Vérifier les conditions aux limites statiques.
- Vérifier les équations d'équilibre.
- Calculer les déformations (loi de Hooke).
- Vérifier les équations de compatibilité.
- Calculer le champ des déplacements.
- Vérifier les conditions aux limites cinématiques.
Lorsqu'il n'y a pas de conditions aux limites cinématiques, ce qui arrive assez souvent, on peut éviter le calcul, parfois pénible, du déplacement, mais non les équations de compatibilité : le déplacement doit pouvoir être calculé, même s'il ne l'est pas réellement.
Le cas du bloc pesant est un bon exemple d'application ===>.
Equations de Beltrami
Là encore il est possible de regrouper les étapes 4 et 5 en écrivant directement en fonction des contraintes les équations de compatibilité.
Là encore le calcul est un peu technique, et nous renvoyons le lecteur au polycopié (VI-1.4). On obtient ainsi les équations de Beltrami, expression des équations de compatibilité en fonction des contraintes
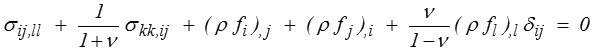
L'apparition des forces de volume dans ces équations tient aux équations d'équilibre qui interviennent dans le calcul. Si les forces de volume sont nulles ou constantes − ce qui est en général le cas − alors ces équations prennent une forme particulièrement simple
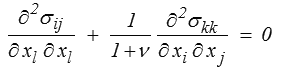
plus sympathique même que les équations de compatibilité originales. Conservons toutefois à l'esprit qu'elles ne s'appliquent qu'en élasticité linéaire isotrope.
Bien évidemment elles sont automatiquement vérifiées si le champ de contrainte est, comme les déformations, fonction linéaire des coordonnées.