Problèmes de MMC
Formulation d'un problème ==>>
Résoudre un problème de MMC c'est, en petites déformations, trouver le déplacement ui ( x , t ) et les contraintes σij ( x , t ) vérifiant en tout point du domaine considéré D
les équations du mouvement
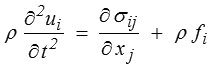
la loi de comportement (relation contraintes-déformations)
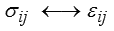
sur sa frontière S = ∂D
des conditions aux limites
et en t = 0
des conditions initiales ui ( x , 0 ) = uid( x )
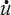i ( x , 0 ) = Vid( x )donnant, comme toujours en mécanique, positions et vitesses à l'instant t = 0.
Très souvent, toutefois, on s'intéressera à des problèmes statiques ou quasi statiques, c'est-à-dire suffisamment lents pour que l'on puisse négliger les termes d'inertie (et donc oublier les conditions initiales).
Problème quasi statique.
Trouver ui ( x ; t ) et σij ( x ; t ) vérifiant
− les équations d'équilibre
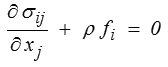
− la loi de comportement,
− les conditions aux limites.
où le temps t n'intervient que paramétriquement (problème quasi statique) voire pas du tout (problème statique). Sauf mention explicite du contraire nous nous limiterons désormais à ce cas.
Conditions aux limites ==>>
Les conditions aux limites traduisent la liaison du solide considéré avec le monde extérieur. Leur choix est une étape importante dans la schématisation d'un problème de mécanique des milieux continus.
Ces conditions aux limites peuvent être complexes (conditions de frottement, contact unilatéral) mais la formulation la plus simple sera celle d'un problème régulier.
Problème régulier.
En chaque point de la frontière il faut se donner 3 composantes complémentaires
du vecteur déplacement
ou
du vecteur des contraintes.
On écrira symboliquement
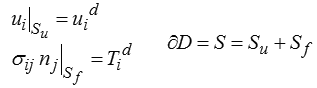
distinguant sur la frontière S = ∂D les endroits où sont donnés les déplacements Su et les efforts Sf (symboliquement, car en réalité Su et Sf peuvent dépendre de la composante considérée). Dans cette écriture uid et Tid représentent des données du problème.
Loi de comportement ==>>
La loi de comportement se traduira mathématiquement par une relation entre le tenseur des contraintes et le tenseur des déformations. Physiquement, c'est par elle qu'interviendront les propriétés et la nature physique du matériau.
Elles peuvent prendre des formes très diverses et leur étude fera l'objet du cours Comportement des Matériaux.
Leur construction et leur identification devront être menées pour chaque matériau et dans des conditions voisines de celles de l'application envisagée, et elles devront s'appuyer sur l'expérience − on parle en général d'essais mécaniques.
L'essai de traction est en Mécanique des Solides le plus largement utilisé et permet assez souvent de conclure, mais il est parfois nécessaire d'utiliser d'autres essais homogènes ou non homogènes.
Deux exemples
A titre d'exemple on peut envisager deux problèmes importants et pour lesquels il est possible d'obtenir, indépendamment de la loi de comportement, des résultats intéressants
Le calcul de structures
Nous nous limitons dans ce cours à la Mécanique des Milieux Continus bi- ou tridimensionnels. En pratique le calcul de structures va utiliser, notamment en fonction de la géométrie du système, bien d'autres modèles monodimensionnels (poutres) ou bidimensionnels (plaques, coques). Les variables de base et les équations correspondantes seront évidemment très différentes, mais on retrouvera, dans la formulation d'un problème, la même structure essentielle :
- Les équations du mouvement (ou d'équilibre),
- La loi de comportement,
- Les conditions initiales (position et vitesse),
- Les conditions aux limites.
Ces dernières auront également la même structure avec, en tout point de la frontière et pour chaque composante, donnée du déplacement ou de l'effort.