Torseurs et Distributeurs
Système de vecteurs
Nous partons d'un système de vecteurs vi ( i = 1, ... n ), chacun de ces vecteurs étant associé à un point Mi de l'espace (on parle souvent de « vecteur lié », car chaque vecteur est attaché, ou lié, à un point). L'exemple le plus naturel est celui d'un ensemble de forces Fi, chacune étant appliquée en un point donné Mi.
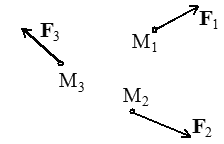
Pour fixer les idées nous avons considéré un ensemble fini ( i = 1, ... n ), mais nous traiterions de la même manière une distribution continue définie par sa densité massique ou volumique. Les sommes finies deviendront alors simplement des intégrales.
On définit la résultante de ce système comme étant la somme vectorielle de tous ces vecteurs
Résultante =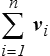 
et le moment en O de ce système est de la même manière défini par
Moment en O =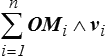 
Torseur
Un torseur est un système de vecteurs pour lequel on ne s'intéresse qu'à la résultante et au moment. Le torseur [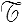
] associé au système de vecteurs ( vi , Mi ) sera donc défini par sa résultante et son moment, que l'on notera
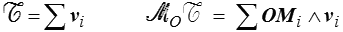
D'un point de vue physique, cela signifie que deux systèmes de vecteurs conduisant à la même résultante et au même moment, donc au même torseur, seront, vis-à-vis de l'énoncé où le mot « torseur » est utilisé, indiscernables.
A titre d'exercice nous laissons au lecteur le soin de vérifier que les trois systèmes de vecteurs ci-dessous correspondent tous au torseur nul :
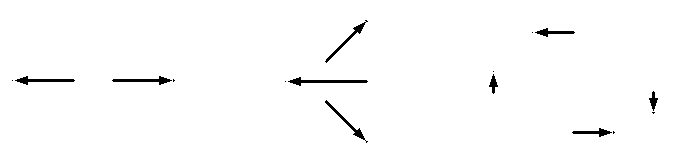
En termes mathématiques on dira que deux systèmes de vecteurs sont équivalents s'ils ont même résultante et même moment, et un torseur est une classe d'équivalence pour cette relation. L'espace des torseurs est alors l'espace quotient correspondant.
Comment choisir le point O ? Fort heureusement cela n'a aucune importance : si l'on choisit en effet un autre point A alors cela ne change évidemment rien à la résultante, tandis que le moment devient
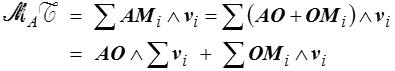
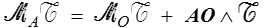
de sorte que si deux systèmes ont la même résultante et le même moment en un point quelconque, ils auront aussi le même moment en tout point de l'espace.
Formule de transport des moments.
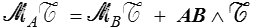
Il en résulte également qu'un torseur est complètement défini par deux vecteurs : sa résultante et son moment en un point. L'espace des torseurs est un espace vectoriel de dimension 6.
Glisseur, couple, axe central
Si l'on peut trouver un point où le moment est nul, on parlera d'un glisseur, tandis que si la résultante est nulle on parlera d'un couple (le moment ne dépend pas du point). Dans le cas général, on définit l'axe central du torseur comme la droite sur laquelle le moment est colinéaire à la résultante, et on parle parfois d'un « visseur », comme superposition d'un glisseur et d'un couple.
On vérifie également sans peine que le produit scalaire
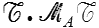
ne dépend pas du point où l'on prend le moment ; cette quantité est appelée invariant du torseur, et elle sera nulle pour un glisseur et pour un couple.
Produit scalaire de deux torseurs
Plus généralement, si [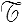1] et [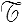2] sont deux torseurs, alors
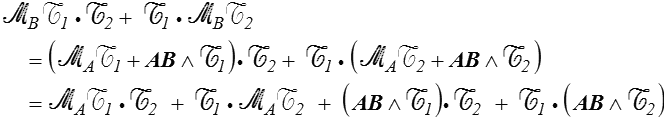
où les deux derniers termes s'annulent en vertu des propriétés du produit mixte
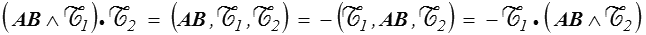
La quantité
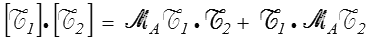
ne dépend pas du point A choisi. Cette quantité est appelée produit scalaire ou comoment des deux torseurs.
J'attire toutefois votre attention sur le fait que ce « produit scalaire » doit être manipulé avec précaution. En particulier, et contrairement à tous ceux que vous avez pu rencontrer jusqu'à présent, il n'est pas associé à une norme. En effet, l'invariant
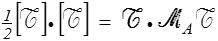
peut être nul sans que le torseur le soit (c'est le cas pour un glisseur comme pour un moment).
Distributeur
Nous sommes partis, pour introduire la notion de torseur, d'un système de vecteurs, par exemple un système de forces. Les vitesses sont bien évidemment un tel système. Peut-on donc parler du torseur des vitesses ? Non, ou, plus exactement, pour obtenir un torseur porteur de sens, il faut pondérer la vitesse par la masse. C'est le torseur des quantités de mouvement ou torseur cinétique (>).
Cependant, dans le cas particulier d'un mouvement de solide rigide, on peut introduire une structure voisine. On démontre en effet que l'on peut calculer la vitesse d'un point M quelconque à partir de celle d'un point particulier et du vecteur rotation. C'est la formule fondamentale de la cinématique du solide rigide (>)
V ( M ) = V ( O ) + Ω ∧ OM
et on constate que cette formule peut être interprétée comme transport du moment pour un torseur distributeur des vitesses défini par
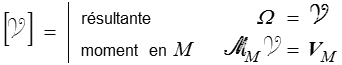
Attention toutefois, une étude plus approfondie montrerait que ces deux notions, torseur et distributeur, ne sont pas exactement identiques, mais duales l'une de l'autre. Je n'insisterai pour l'instant pas davantage sur cet aspect, profond mais subtil, et lié de manière essentielle au fait que nous soyons dans un espace à trois dimensions. L'étude du cas bidimensionnel nous en montrera toutefois quelques symptômes révélateurs.
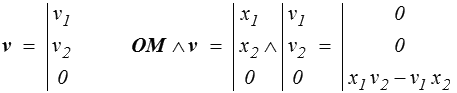
Pour le distributeur des vitesses, au contraire, sa résultante, vecteur rotation, est normale au plan, tandis que son moment est dans le plan
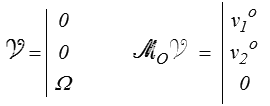
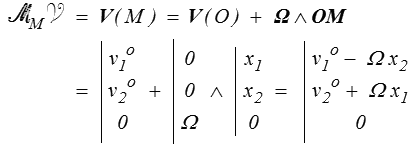
Voilà qui montre bien la différence entre torseur et distributeur.