Elasticité classique
Nous nous limiterons, dans ce cours d'introduction, au modèle élastique linéaire isotrope, le plus simple possible, définissant ainsi le cadre de l'élasticité classique. Bien que très rudimentaire ce modèle reste très largement utilisé car, pour la plupart des matériaux, il peut être utilisé en première approximation sous réserve que les sollicitations appliquées restent faibles.
Le comportement élastique ==>>
La première hypothèse, caractéristique de l'élasticité en fait, est une hypothèse de réversibilité qui suppose
- l'absence de dissipation,
- une relation biunivoque entre contrainte et déformation.
Dans un cadre thermodynamique (<) ceci implique l'existence d'une énergie de déformation w ( εij ) permettant d'écrire
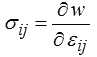
Elasticité linéaire ==>>
La seconde hypothèse suppose que cette relation entre contrainte et déformation est linéaire (dans l'essai de traction, la contrainte est proportionnelle à la déformation, σ = E ε), approximation souvent très raisonnable. Ceci conduit à une relation
σij = Aijkl εkl ou εij = Sijkl σkl
introduisant, pour expliciter cette relation linéaire, un tenseur du 4ème ordre, le tenseur d'élasticité Aijkl, ou, par inversion, le tenseur de souplesse Sijkl.
Loi de Hooke ==>>
Cette relation peut sembler compliquée, mais elle se simplifie considérablement si l'on fait de plus l'hypothèse d'isotropie (le matériau a les mêmes propriétés dans toutes les directions). Elle devient alors simplement
σij = λ εkk δij + 2 μ εij
loi de Hooke, qui introduit deux coefficients matériels λ et μ (constantes de Lamé). L'écriture inverse
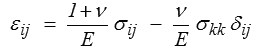
souvent plus commode, fait intervenir deux autres coefficients (différents de λ et μ, mais qui leur sont bien évidemment reliés) dont la signification physique apparaît clairement en traction simple (<)
- E : module d'Young, coefficient de proportionnalité entre contrainte et déformation, σ = E ε,
- ν : coefficient de Poisson, coefficient de proportionnalité entre contraction transversale et allongement longitudinal, εt = ν ε (<).
Une troisième écriture, la plus simple (mais pas nécessairement la plus commode), découple cette loi en deux relations scalaires entre déviateur et partie sphérique ((<), (<))
σkk = 3 K εkk sij = 2 G eij
Critère de limite d'élasticité ==>>
S'il couvre un champ très large d'applications, ce modèle est en contrepartie toujours limité. Son utilisation devra donc toujours être complétée par la vérification a posteriori du fait que l'on est bien resté dans son domaine de validité. C'est le critère de limite d'élasticité qui traduit cette condition et qui, in fine, conduira au dimensionnement d'une structure.
Il dépend bien évidemment très fortement du matériau considéré, mais pour les matériaux métalliques on utilisera très souvent le critère de von Mises
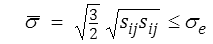
La contrainte équivalente de von Mises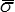 
doit rester inférieure à la limite élastique σe en traction simple.
Problèmes d'élasticité ==>>
Ceci étant fait, nous pouvons enfin aborder la formulation, et éventuellement la résolution, d'un problème aux limites. Le résultat essentiel est ici le fait qu'un problème régulier est, dans ce cadre, bien posé, c'est-à-dire qu'il existe une solution et qu'elle elle est unique. (En fait, c'est un résultat valable pour l'élasticité linéaire, l'isotropie n'est pas ici essentielle).
Malheureusement on ne saura déterminer explicitement cette solution, que l'on sait exister et être unique, que dans quelques cas très particuliers. Il faudra en général faire appel à des méthodes approchées et/ou numériques.
Les quelques solutions que l'on sait construire ne permettent de traiter que des problèmes très simples ; elles sont néanmoins fort instructives et il est intéressant d'en étudier quelques-unes, ce qui nous permettra par la même occasion d'introduire quelques outils généraux (équations de Navier et de Beltrami, en particulier).