Système de particules
Le modèle physique
Nous nous intéressons à la mécanique d'un système de N particules en interaction, et nous notons xi(t) = OMi le vecteur définissant à chaque instant la position de la particule numéro i (i = 1 à N).
L'équation du mouvement de cette particule s'écrit (<)
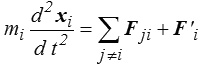
où mi est la masse de la particule et où on a noté
Fji : la force d'interaction exercée sur la particule i par la particule j,
F'i : la force exercée sur la particule i par le monde extérieur.
Les Fji et les F'i sont respectivement appelés efforts intérieurs et efforts extérieurs. Insistons à nouveau sur le caractère relatif et conventionnel de cette terminologie. Les « efforts intérieurs » sont bien évidemment « extérieurs » pour la particule considérée. Nous sommes toutefois ici dans un cas où cette terminologie est, bien que relative, tout à fait naturelle.
L'interaction entre particules sera prise sous la forme
Fji = f ( rij ) uij = − Fij
Mi Mj = xj − xi = rij uij
où rij est la distance Mi Mj et uij est le vecteur unitaire dans la direction Mi Mj.
La fonction scalaire f(r) caractérise la loi d'interaction avec la convention usuelle ( f positif si attraction, négatif si répulsion), mais cela n'a guère d'importance pour la suite.
Remarquons que, en tant que description de la matière, ce modèle est relativement simpliste puisque :
- D'une part il se situe dans le cadre de la mécanique newtonienne alors que, à cette échelle moléculaire, les effets quantiques jouent un rôle. C'est néanmoins une hypothèse courante qui conduit, entre autres, à la dynamique moléculaire. (w)
- D'autre part il est limité à l'interaction de paire, alors que les interactions entre trois particules, notamment angulaires, sont souvent très importantes.
La loi fondamentale
Le mouvement du système résulte alors de l'intégration de ce système d'équations et nécessite une connaissance précise de la loi d'interaction. Il est cependant possible de construire, par combinaison linéaire, 6 équations scalaires faisant disparaître les efforts intérieurs.
En effet, si l'on fait la somme de toutes ces N équations on obtient
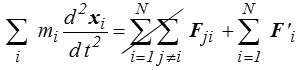
et les efforts intérieurs disparaissent puisque Fij = −Fji . C'est le théorème du centre d'inertie.
De la même manière le moment dynamique s'obtiendra en faisant la somme
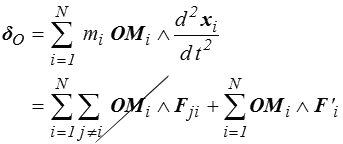
car on constate que les termes d'efforts intérieurs s'éliminent deux à deux
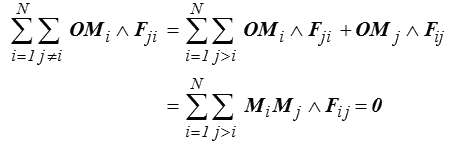
puisque Fij = −Fji est colinéaire à Mi Mj.
Pour déterminer complètement le mouvement du système il faut connaître les efforts intérieurs et intégrer 3N équations différentielles, mais dans les 6 équations
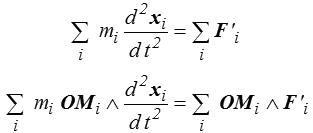
les efforts extérieurs apparaissent seuls. C'est la loi fondamentale (<) qui se présente donc simplement comme six combinaisons linéaires des équations du mouvement dans lesquelles les efforts intérieurs disparaissent (et ce sont bien les seules).
Puissances virtuelles
Le théorème des puissances virtuelles (<) s'obtient en multipliant (produit scalaire) l'équation du mouvement de chaque particule par un vecteur arbitraire que l'on notera V *i et que l'on appellera « vitesse virtuelle ». On fait ensuite la somme de toutes ces équations pour obtenir
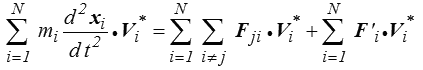
Le dernier terme est appelé « puissance virtuelle » des efforts extérieurs (puisque somme de produits d'une force par une « vitesse virtuelle »). Par analogie, on appellera puissance virtuelle des quantités d'accélération le premier membre et « puissance virtuelle des efforts intérieurs» le premier terme du second membre.
Théorème des puissances virtuelles.
La « puissance virtuelle » des quantités d'accélération est égale à la « puissance virtuelle » des efforts extérieurs plus la « puissance virtuelle » des efforts intérieurs.
L'expression de la puissance virtuelle des efforts intérieurs peut, en regroupant les termes par paire, se transformer en
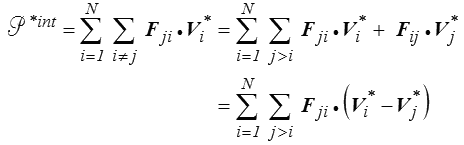
de sorte que finalement
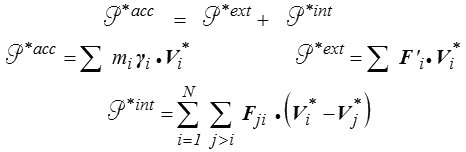
Comme nous l'avons indiqué plus haut (<) Le théorème des puissances virtuelles correspond en fait à ce que les mathématiciens appellent une formulation faible. La configuration du système est définie par les 3N variables définissant la position de chaque particule : l'espace des configurations est un espace vectoriel de dimension 3N et les équations du mouvement de chaque particule définissent dans cet espace une équation différentielle vectorielle contrôlant le mouvement (formulation forte). La « formulation faible » s'obtient en faisant le produit scalaire de cette équation vectorielle par un vecteur arbitraire et c'est bien ce que − à la terminologie près − nous avons fait. Dans un espace de dimension finie, comme c'est le cas ici, ces deux formulations sont complètement équivalentes et l'on peut prendre la loi des puissances virtuelles comme loi physique première (on parle alors de « principe des puissances virtuelles » et la loi fondamentale devient alors un théorème).
Théorème des travaux virtuels
Puisque l'ensemble des V *i définit en fait un vecteur arbitraire, on peut tout aussi bien les noter u*i ou δu i et les nommer « déplacements virtuels ». On obtient ainsi le théorème des travaux virtuels
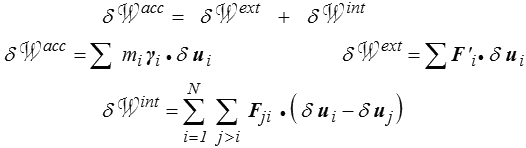
Le travail virtuel des quantités d'accélération est égal au travail virtuel des efforts extérieurs plus le « travail virtuel des efforts intérieurs ».
Ce n'est bien évidemment là qu'un changement de terminologie et de notation.
Formalisme hamiltonien
La force d'interaction interparticulaire dérive d'un potentiel. En effet, si l'on introduit la fonction w primitive de f
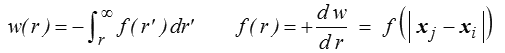
on peut alors écrire directement
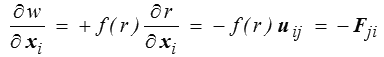
Il est donc naturel de prendre comme énergie potentielle
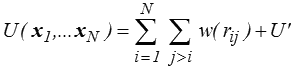
où U' est l'énergie potentielle des efforts « extérieurs » (eux aussi supposés dérivant d'un potentiel).
En tant que système mécanique nous avons affaire à un système discret à 3N degrés de liberté, les positions x i des N particules. L'énergie cinétique est bien évidemment
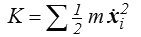
L'écriture des équations de Lagrange
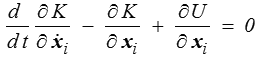
conduit alors directement à l'équation du mouvement pour particule i
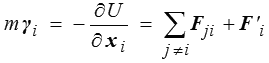
Comme nous l'avons annoncé, le principe de moindre action s'applique tout naturellement. On peut préférer son élégance à l'écriture directe des lois de Newton, mais il n'apporte rien de nouveau.
Un modèle plus général
Comme nous l'avons signalé plus haut, le modèle que nous avons construit était limité aux interactions de paires. On peut en fait construire un modèle plus général, et cette construction nous permettra d'éclairer et d'illustrer deux importants aspects déjà annoncés mais sans justification.
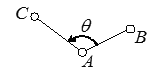Nous avons par exemple mentionné l'interaction angulaire fréquente dans de nombreux cristaux, ce qui correspond à une énergie d'interaction du type
w = ½ k ( θ − θo ) 2
où θo est la valeur de l'angle (AB , AC) à l'équilibre. Techniquement on pourra évaluer cet angle à partir du produit scalaire AB . AC, et donc de la position des trois particules A, B et C. Nous sommes par contre bien en peine d'en tirer la force d'interaction induite sur la particule A.
Pour être plus général encore, et sans avoir à rentrer dans le détail du calcul, nous supposerons que l'énergie potentielle associée à toutes les interactions entre les particules de notre système peut s'écrire sous la forme
U int = U int( x1 , x2 ,... xN )
de sorte que l'énergie potentielle totale est
U( x1 , x2 ,... xN ) = U int + U'
Il est bien entendu que la distinction entre l'énergie potentielle des efforts extérieurs et celle des efforts d'interaction (donc intérieurs) semble à ce stade très artificielle. Elle est néanmoins essentielle, comme nous le verrons plus loin.
Le principe de moindre action donne alors directement
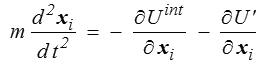
Nous avons annoncé plus haut que le principe de moindre action pouvait dans certains cas être mieux approprié que l'approche directe. Nous en avons ici un exemple probant. Dans le cadre d'une approche directe, nous aurions certes pu suivre les physiciens en affirmant que, une fois connu le potentiel, la force en découle directement par dérivation, mais la signification mécanique de cette dérivation reste mystérieuse, par exemple dans le cas d'une interaction angulaire.
Homogénéité de l'espace
Cette hypothèse consiste à dire que l'espace a les mêmes propriétés en tout point, c'est-à-dire en fait que les lois de la physique sont les mêmes à Ecully, à Moscou, sur la Lune ou en un point éloigné de la galaxie (à condition bien sûr de travailler en repère galiléen, ce que nous avons supposé depuis le départ).
Pour notre problème ceci se traduit simplement par le fait que si l'on déplace de la même quantité toutes les particules qui constituent notre système cela ne change rien à leur interaction et donc que
U int( x1 + a , x2 + a ,... xN + a ) = U int( x1 , x2 ,... xN )
Attention, c'est ici qu'intervient la différence entre potentiel d'interaction et potentiel des efforts extérieurs − la gravité, exemple typique d'efforts extérieurs, n'est pas la même sur la Terre et sur la Lune. Si maintenant nous différentions cette identité par rapport au vecteur a, il vient directement
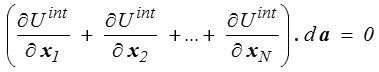
pour tout vecteur da et il vient donc
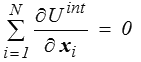
de sorte que, comme dans le cas des interactions de paires, les efforts intérieurs disparaissent lorsque l'on fait la somme des équations du mouvement pour toutes les particules.
C'est le théorème du centre d'inertie qui est donc bien comme nous l'avons annoncé une conséquence de l'homogénéité de l'espace.
Isotropie de l'espace
De la même manière, l'espace a les mêmes propriétés dans toutes les directions, notre énergie d'interaction sera donc inchangée si l'on impose la même rotation à toutes les particules,
U int( Q x1 , Q x2 ,... Q xN ) = U int( x1 , x2 ,... xN )
où Q est une rotation (c'est-à-dire une application linéaire orthogonale, Q Q T ). On démontre alors de la même manière (mais au prix de quelques efforts!) en dérivant par rapport à Q que
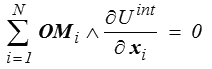
et donc que les efforts intérieurs disparaissent dans le théorème du moment cinétique. La loi fondamentale traduit donc bien, comme annoncé, l'homogénéité et l'isotropie de l'espace.