Compression frettée
Formulation du problème
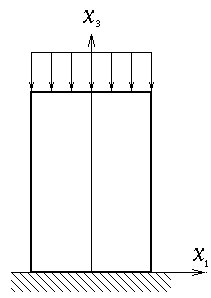
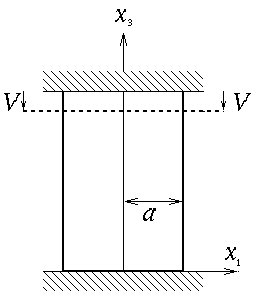 Ce problème correspond à l'écrasement d'un bloc cylindrique de hauteur h et de section S (circulaire de rayon a par exemple, mais peu importe en fait).
Ce problème correspond à l'écrasement d'un bloc cylindrique de hauteur h et de section S (circulaire de rayon a par exemple, mais peu importe en fait).
La surface latérale est libre de contrainte
σij nj |Slat = 0
La face inférieure est complètement bloquée tandis que l'on impose à la face supérieure un déplacement vertical V mais en interdisant tout déplacement transversal (c'est justement cette condition de non glissement sur les deux plateaux de la presse qui différencie cet essai de l'essai de compression simple (<); elle correspond par exemple à un frottement infini ou à un contact adhérent).
So : x3 = 0 u1 = u2 = u3 = 0
S1 : x3 = h u1 = u2 = 0 u3 = −V
Il s'agit bien évidemment d'u problème régulier. On s'intéresse en particulier à la force d'écrasement nécessaire P et à la rigidité de la structure k qui, une fois le problème résolu, s'obtiendront en écrivant
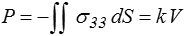
Recherche d'une solution homogène
On recherche une solution homogène (<) (contraintes et déformations constantes). Les conditions aux limites en déplacements imposent alors

et donc
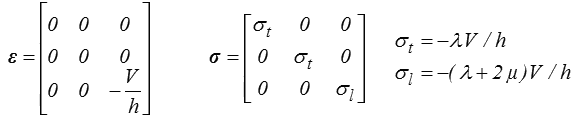
Or les conditions aux limites sur la surface latérale imposent
σl = −λ V / h = 0
Cette solution ne convient que si λ = 0 c'est-à-dire pour ν = 0, μ = E / 2. La rigidité de la structure vaut alors
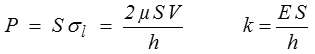
Théorème d'encadrement
Dans le cas général (ν ≠ 0), et faute de pouvoir trouver la solution exacte, nous pouvons appliquer le théorème d'encadrement. Les efforts donnés (forces de volume et surface latérale) sont nuls, tandis que le seul déplacement donné non nul est V.
Le théorème de comparaison (<) s'écrit donc
− 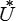 (
( 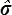 ) = − W (
) = − W ( 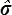 ) +
) + 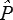 V ≤ −
V ≤ − 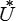 ( σ ) = U ( u ) ≤ W (
( σ ) = U ( u ) ≤ W ( 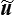 ) = U (
) = U ( 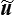 )
)
et pour la solution
− 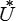 ( σ ) = U ( u ) = − W + P V = W = ½ P V
= ½ k V 2
( σ ) = U ( u ) = − W + P V = W = ½ P V
= ½ k V 2
soit encore un encadrement de la rigidité
− W 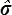 ) +
) + 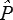 V ≤ ½ k V 2 ≤ W (
V ≤ ½ k V 2 ≤ W ( 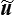 )
)
mais avec ici une énergie potentielle positive pour la solution.
Une borne supérieure
Le champ de déplacement

n'est solution que pour ν = 0. Dans le cas général ce sera un CCA.
Pour calculer son énergie de déformation on peut partir de la définition générale
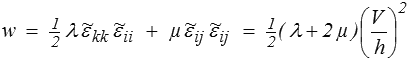
mais il est plus simple de partir de la relation
w = ½ 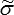 ij
ij 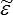 ij = ½
ij = ½ 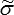 l
l 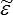 33
33
où 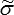 ij dénote la contrainte calculée à partir de
ij dénote la contrainte calculée à partir de 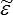 ij par la loi de Hooke (qui n'est bien évidemment pas CSA, d'où la notation). L'énergie s'obtient en multipliant par le volume S h
ij par la loi de Hooke (qui n'est bien évidemment pas CSA, d'où la notation). L'énergie s'obtient en multipliant par le volume S h
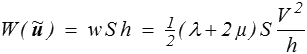
et le théorème de l'énergie potentielle donne
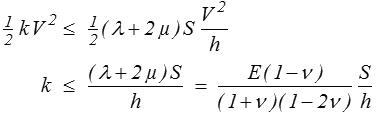
C'est en fait la rigidité que nous avions obtenue pour l'essai dométrique (<) et qui apparaît ici comme borne supérieure.
Une borne inférieure
De la même manière nous cherchons un CSA homogène. Les conditions aux limites sur la surface latérale imposent alors
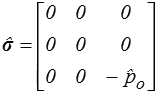
Son énergie complémentaire sera alors
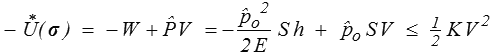
On obtient ainsi pour toute valeur de la constante 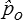 une borne inférieure. Nous choisirons la plus grande en écrivant
une borne inférieure. Nous choisirons la plus grande en écrivant
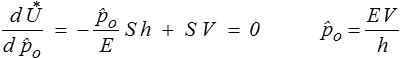
Remarquons que cette valeur pouvait sans doute être assez facilement devinée puisque notre CSA correspond à un état de compression simple (<). La démarche normale consiste toutefois bien à chercher la valeur optimale. Nous obtenons ainsi comme borne inférieure
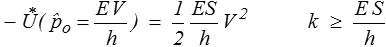
Encadrement de la rigidité
Nous avons donc obtenu facilement un encadrement de la rigidité
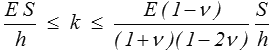
Pour ν = 0, ces deux bornes coïncident bien évidemment puisque nous avions alors obtenu la solution exacte.
La borne supérieure devient très grande pour un matériau peu compressible (ν 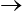 1/2). Pour ν = 1/4, par exemple, il vient
1/2). Pour ν = 1/4, par exemple, il vient
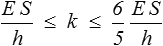
soit une approximation intéressante.
Efforts imposés
 Considérons maintenant un problème similaire mais à effort imposé. Les conditions aux limites sont alors
Considérons maintenant un problème similaire mais à effort imposé. Les conditions aux limites sont alors
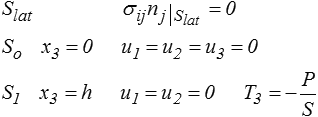
avec un effort imposé P. On obtiendra alors
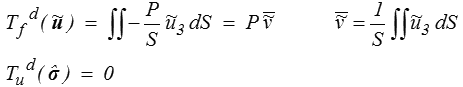
et le théorème de comparaison s'écrira
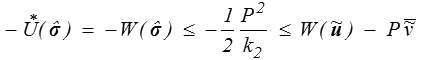
où la rigidité k2 est définie par
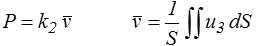
L'énergie encadrée est négative, mais on obtiendra néanmoins, comme pour notre problème modèle (<), une borne inférieure pour tout CSA et une borne supérieure pour tout CCA.
Je laisse au lecteur le soin d'utiliser des CCA et CSA homogènes pour vérifier que l'on obtient en fait le même encadrement. Ces deux problèmes sont toutefois différents et on peut d'ailleurs montrer que le second problème conduit à une rigidité plus faible
k2 ≤ k
Comment peut-on démontrer ce résultat ?
En prenant par exemple la solution du problème 2 comme CSA pour le problème 1, ou bien la solution du problème 1 comme CCA pour le problème 2.
