Théorèmes de l'énergie
Plus généralement on regroupe traditionnellement sous le vocable « Théorèmes de l'énergie » divers théorèmes universellement valables en élasticité linéaire. Rappelons ici que tous le résultats de ce chapitre pourront s'appliquer immédiatement pour d'autres modèles, sitôt que l'on aura établi pour eux le diagramme rectangulaire (<) associé.
Théorème du travail
Théorème du travail.
Pour la solution ( ui , σij ) d'un problème régulier le travail des efforts extérieurs est égal à deux fois l'énergie de déformation
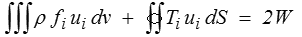
La démonstration découle directement du lemme fondamental (<) appliqué à σij et ui
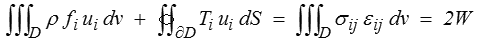
puisque la densité d'énergie élastique est en élasticité linéaire
w = ½ σij εij
Le coefficient 2 peut surprendre. Il provient du fait que le « travail » évoqué ici est le travail des efforts extérieurs dans les déplacement finaux après application des efforts, alors que ceux-ci ne sont appliqués que progressivement. Le cas du ressort linéaire
F = k x dW = F dx => W = ½ k x2 = ½ F x
montre bien l'origine de ce coefficient 2.
Théorème de comparaison
Il en résulte que pour la solution
U ( u ) +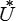 
( σ ) = 2 W − Tfd( u ) − Tud( σ ) = 0
Ceci permet de regrouper le théorème de l'énergie potentielle et le théorème de l'énergie complémentaire.
Théorème de comparaison.
Pour tout CSA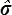 
et tout CCA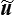 
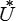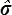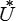− ( ) ≤ − ( σ ) = U ( u ) ≤ U ( )
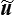Ainsi tout CSA donne une borne inférieure et tout CCA une borne supérieure de l'énergie potentielle de la solution. Leur combinaison permet donc un encadrement de cette quantité. On verra sur divers exemples que cette quantité encadrée est liée à la rigidité de la structure: tout CCA donne une borne supérieure de la rigidité, tout CSA une borne inférieure. C'est une première utilisation de ces théorèmes variationnels qui permettent d'évaluer la rigidité de la structure ainsi que la qualité de cette évaluation.
Application
Revenant à notre problème modèle (<), on peut écrire pour la solution
U ( u ) = W − Tfd( u ) = − 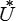( σ ) = −W
soit, en prenant la demi-somme de ces deux expressions égales,
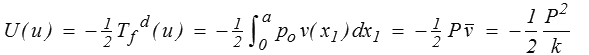
où P = po a est la charge appliquée sur la face supérieure (par unité d'épaisseur) et où l'on a noté v ( x1 ) = −u2 (x1 , a) le déplacement vertical (vers le bas) de la face supérieure et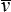 
sa valeur moyenne. La quantité k = P / 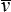est une mesure de la rigidité de la structure.
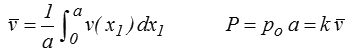
Le théorème de comparaison nous donne donc pour tout CSA 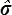et tout CCA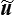
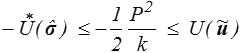
Si l'on reporte les valeurs obtenues précédemment pour ν = 1/4, on trouve
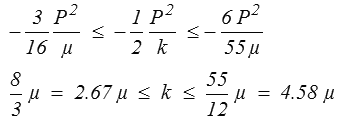
un encadrement très grossier, mais qui nous garantit un ordre de grandeur.
Ceci correspond à un encadrement de la rigidité k par en dessous pour le CSA et par au-dessus pour le CCA.
Un exemple : la compression frettée (===>)
Dans l'exemple précédent on a obtenu une énergie potentielle négative et une énergie complémentaire positive. Ce sera en général le cas pour un problème à efforts imposés. On obtient par contre une situation symétrique pour un problème à déplacements imposés. L'exemple de la compression frettée (compression d'un bloc entre les deux plateaux d'une presse en interdisant tout glissement) est représentatif.
Théorème de réciprocité
Nous considérons maintenant une structure (donc ici un domaine D) pouvant être soumise à deux chargements différents. On note ( u 1, σ 1) et ( u 2, σ 2) les solutions des deux problèmes réguliers correspondants.
Théorème de Maxwell-Betti (ou de réciprocité).
Le travail des efforts extérieurs du problème 1 dans la solution u 2 est égal au travail des efforts extérieurs du problème 2 dans la solution u 1
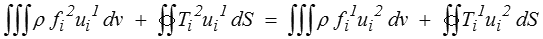
Ce résultat résulte du théorème des travaux virtuels appliqué une première fois au problème 1 avec comme déplacement virtuel la solution du problème 2, puis une seconde fois en échangeant les rôles de 1 et 2.
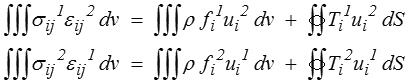
Mais, compte tenu de la symétrie de l'opérateur d'élasticité,
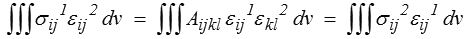
d'où la conclusion.
Ce théorème, utilisé de manière astucieuse, donne parfois des résultats intéressants en MMC, mais il trouvera sa pleine importance en Résistance des Matériaux.
On remarquera aussi que ce théorème fait intervenir les efforts (donnés ou non) exercés sur toute la surface. Il faudra donc dans chaque cas l'adapter en fonction des conditions aux limites spécifiques (efforts ou déplacements donnés).
Théorème de Castigliano
Terminons, pour être complet, par un résultat que je n'ai jamais vu utilisé en MMC, mais qui le sera de manière tout à fait essentielle en RdM. Il importe donc de le mentionner ici, dans une présentation générale des théorèmes de l'énergie.
Nous considérons encore une structure soumise à deux chargements différents, mais nous supposons de plus que ces deux chargements ne diffèrent que par les efforts appliqués sur Sf et éventuellement les forces de volume (même Su et mêmes déplacements donnés), de sorte que les deux problèmes correspondants admettent les mêmes CCA.
Théorème de Castigliano.
Dans ces conditions, si 
ij2 est CSA pour le problème 2, le travail des efforts 2 dans les déplacements u 1 est donné par
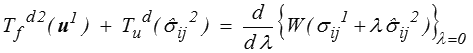
Pour démontrer ce théorème, on développe
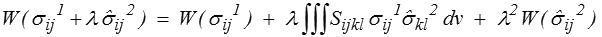
de sorte que
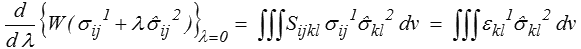
D'où la conclusion, en appliquant le lemme fondamental (<) au problème 2 pour lequel ij2 est CSA par hypothèse, tandis que u 1 est CCA d'après les hypothèses faites sur Su et les déplacements donnés.