Hydrostatique
Pression hydrostatique
L'hydrostatique s'intéresse, comme son nom l'indique, à un fluide − typiquement de l'eau (hydro) − au repos (statique).
Nous reviendrons souvent dans la suite sur la définition d'un fluide − c'est en fait une question beaucoup plus subtile qu'il n'y paraît, la réponse ultime vous surprendra je pense. Pour l'instant nous partirons de la propriété suivante.
Propriété.
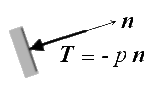
Un fluide au repos exerce sur toute surface une pression p normale à cette surface.
Le vecteur contrainte peut donc s'écrire
T(x,n) = − p(x,n) n (dF = − pn dS)
Mais en chaque point x ce vecteur peut aussi s'obtenir à partir du tenseur des contraintes
T(x,n) = σ(x) n
Il en résulte que tout vecteur n est vecteur propre du tenseur des contraintes et donc que les trois contraintes principales sont égales
T(x,n) = − p(x) n σij = − p δij
La pression p est la même dans toutes les directions, c'est la pression hydrostatique (avec un signe moins du fait de la convention de signe choisie).
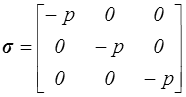
Répartition de la pression
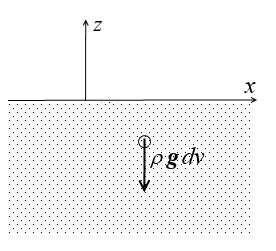Pour un fluide pesant les forces de volume sont (en prenant l'axe z = x3 selon la verticale ascendante) données par
f = g = − g e3
En reportant dans les équations d'équilibre il vient
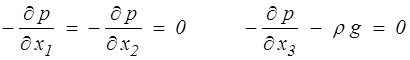
En supposant la masse volumique constante, ces équations s'intègrent directement pour donner
p = − ρgx3 + Cte
La constante d'intégration s'obtient en écrivant que sur la surface libre, choisie comme origine de l'axe vertical, x3 = 0, la pression est nulle, plus exactement égale à la pression atmosphérique, mais celle-ci sera − souvent en mécanique des fluides et toujours en mécanique des solides − prise nulle par convention (>) . Donc finalement
p = − ρgx3
Ceci montre en particulier, s'il en était besoin, que la surface libre est nécessairement horizontale.
Théorème d'Archimède
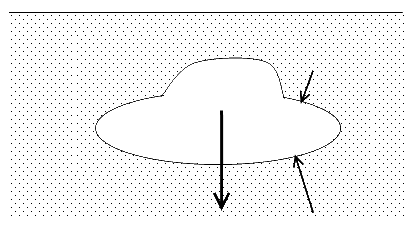Considérons un solide D complètement immergé dans un fluide. La poussée d'Archimède, effort exercé par le fluide que le solide, est donnée par
Théorème d'Archimède.
Le torseur des efforts exercés par le fluide sur le solide est équivalent à une force ρgV appliquée au centre géométrique du volume V occupé par le solide.
ou comme on le dit usuellement au poids du fluide déplacé.
On peut donner de ce résultat deux démonstrations. La première, astucieuse, remarque que cet effort est complètement déterminé par la répartition de pression obtenue plus haut, et donc indifférent à la présence ou à l'absence du solide immergé. Si l'on remplace le solide par le fluide qu'il a déplacé, ce volume de fluide sera bien sûr en équilibre. Le torseur des efforts de pression exercés sur la frontière de D équilibre donc le poids du fluide contenu à l'intérieur.
La seconde démonstration, plus technique et laborieuse, est néanmoins instructive, et constitue un bon exercice.
Pour la résultante on écrit
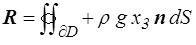
soit, en utilisant le théorème de la divergence (<) ,
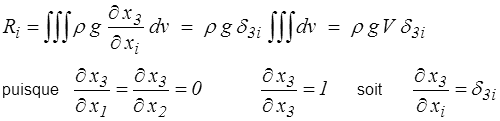
Donc finalement
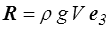
Pour le moment, c'est un peu plus long
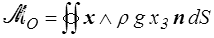
soit en composantes
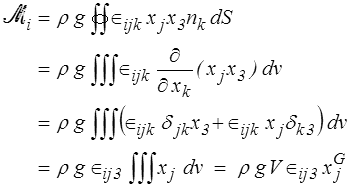
en introduisant G centre (d'inertie) géométrique du volume occupé par D. On obtient donc finalement
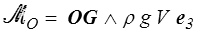
moment en O du poids de l'eau (qui occuperait le domaine D) ρ g V appliqué en G.
Statique de l'atmosphère
Pourquoi parle-t-on d'hydrostatique plutôt que de statique des fluides ? En d'autres termes, en quoi l'hydrostatique se différentie-t-elle de l'aérostatique, statique de l'air, ou plus généralement des gaz ? La raison en est dans l'hypothèse faite plus haut lorsque nous avons supposé ρ constant (fluide incompressible). Si la masse volumique ρ n'est plus constante, on peut toujours écrire
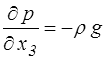
mais pour intégrer cette équation différentielle il faut connaître ρ en fonction de x3. Or cette masse volumique dépendra elle-même de la pression (et aussi de la température). Il faudrait compléter cette équation par la loi d'état du gaz. Ce problème, essentiel pour l'étude de l'atmosphère, est actuellement hors de notre portée.