Torsion d'un arbre cylindrique
Un champ de contrainte
Considérons le champ de contrainte défini dans un système de coordonnées cartésiennes (x1, x2, x3 ) par
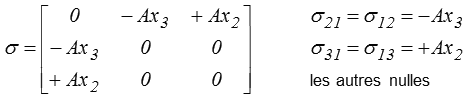
où A est une constante. On vérifie directement que
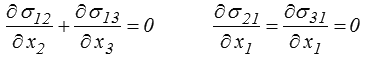
et les équations de l'équilibre sont vérifiées avec des forces volumiques nulles.
Pour mieux comprendre le sens physique de cette solution, nous allons caractériser les efforts exercés sur un barreau cylindrique de révolution d'axe x1 (rayon a, longueur l).
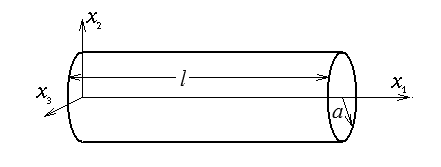
 Sur la surface latérale
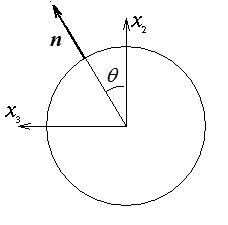
Sur la surface latérale
x2 = a cos θ x3 = a sin θ
la normale extérieure est
n = ( 0, cos θ, sin θ )
Le vecteur contrainte est T = σ n
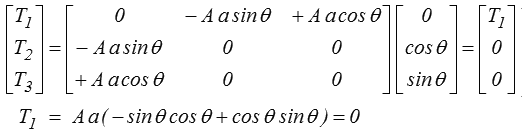
La surface latérale est libre de contrainte. Le cylindre n'est sollicité que sur ses deux sections d'extrémités x1 = 0 et x1 = l.
Pour x1 = l, par exemple, n = ( 1, 0, 0 ) et le vecteur contrainte est
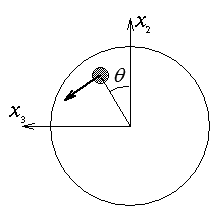
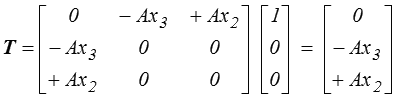
Il s'agit d'une contrainte de cisaillement et elle est, en chaque point de la section, orthoradiale. Pour dégager la signification des ces efforts, nous allons avaluer leur torseur. La résultante est nulle
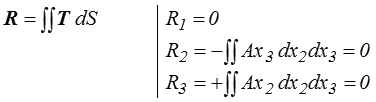
les deux dernières intégrales étant nulles par symétrie (ou, pour les sceptiques, par calcul direct des intégrales de surface). Le moment au point C, centre de la section, est de même donné par
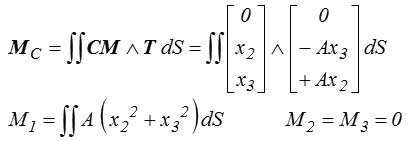
Pour calculer la première intégrale il est commode d'utiliser les coordonnées polaires
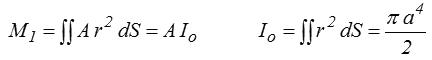
Io est appelé moment d'inertie polaire de la section.
 On trouve de la même manière que le torseur des efforts exercés sur la section x1 = 0, n = (−1, 0, 0 ), est un couple − A Io e1 (et qui équilibre le couple exercé à l'autre extrémité, les équations différentielles d'équilibre assurent évidemment l'équilibre global).
On trouve de la même manière que le torseur des efforts exercés sur la section x1 = 0, n = (−1, 0, 0 ), est un couple − A Io e1 (et qui équilibre le couple exercé à l'autre extrémité, les équations différentielles d'équilibre assurent évidemment l'équilibre global).
Ainsi notre barreau est soumis à l'action d'un couple autour de son axe. C'est ce que l'on appelle une sollicitation de torsion.
Un champ de déplacement
D'un point de vue expérimental on pourra par exemple fixer l'extrémité x1 = 0 et imposer le couple de torsion M à l'autre extrémité. L'expérimentation (ou l'intuition) suggère alors que chaque section x1 = Cte tourne autour de x1 d'un angle φ proportionnel à la distance
φ = α x1 α = Δø / l
si Δø est l'angle de rotation de la section d'extrémité, et où α (rotation par unité de longueur) est appelé angle unitaire de torsion.
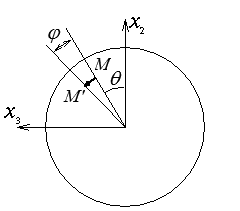 Le déplacement d'un point M sera alors donné par
Le déplacement d'un point M sera alors donné par
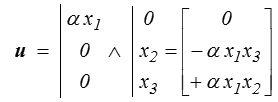
On est donc naturellement amené à postuler un champ de déplacement sous la forme
u1 = 0 u2 = − α x1 x3 u3 = α x1 x2
Le tenseur des déformations s'obtient alors directement à partir de sa définition, par exemple
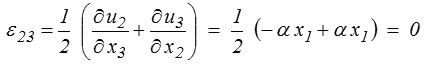
et finalement
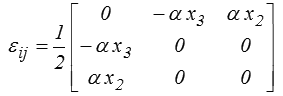
et on vérifie directement que ce champ, linéaire par rapport aux coordonnées, vérifie les équations de compatibilité (<). En fait il n'y avait d'ailleurs rien à vérifier, puisque ces équations de compatibilité expriment l'existence d'un champ de déplacement. Or nous sommes justement partis d'un champ de déplacement, elles sont donc automatiquement vraies et il est inutile de les vérifier.
Sollicitation de torsion
On constate que les deux champs (contrainte et déformation) que nous venons de construire sont proportionnels l'un à l'autre. Peut-il s'agir d'un résultat général ?
Certes non, car c'est la loi de comportement qui donne la relation entre contraintes et déformations. Ceci ne pourra donc convenir que si la loi de comportement exprime justement une telle proportionnalité, ce qui constituera incontestablement un cas intéressant (et nous y reviendrons), mais particulier.
Que se passe-t-il donc en torsion dans le cas général ? On ne peut pas avoir simultanément contraintes et déformations données par les formules précédentes, et on ne peut, au mieux, que garder l'un ou l'autre. Lequel ?
C'est l'analyse du mouvement (déplacement et déformation) qu'il faut conserver. On peut invoquer pour cela deux arguments.
- C'est un raisonnement qui nous y a conduits, alors que le champ de contrainte a été postulé arbitrairement. Certes ce raisonnement est basé sur une hypothèse physique, mais cette dernière est porteuse de sens et vérifiable expérimentalement.
- Nous avons remarqué que le champ de déformation obtenu vérifiait les équations de compatibilité. Si par contre nous partons du champ de contrainte, les déformations que l'on en tirerait par écriture de la loi de comportement n'ont plus aucune raison de satisfaire ces équations de compatibilité.
En fait, le champ cinématique postulé correspond bien à la solution générale du problème de torsion, sous réserve du moins que la loi de comportement respecte elle aussi la symétrie de révolution du problème.
Utilisation des coordonnées cylindriques
Le lecteur économe de ses efforts se demande peut-être pourquoi on a travaillé ici en coordonnées cartésiennes alors que, compte tenu de la symétrie de révolution, il serait sans doute plus commode d'utiliser les coordonnées cylindriques (<) : il a bien raison.
En coordonnées cylindriques ( r, θ, z ) le champ de contrainte s'écrit alors
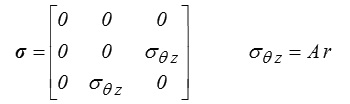
et l'on peut reprendre directement les calculs faits plus haut en remarquant que sur la surface latérale n = er , tandis que sur la section z = l, n = ez . Il faut par contre prendre soin, pour vérifier les équations d'équilibre, de les écrire en coordonnées cylindriques (<).
De même, le déplacement peut être écrit
ur = uz = 0 uθ = α r z
et, en utilisant les formules de calcul des déformations en coordonnées cylindriques (<) , il vient
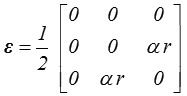
résultat qui restera vrai en général, tandis que le tenseur des contraintes aura la structure donnée plus haut, mais avec une contrainte σθz obtenue à partir de εθz = α r / 2 par écriture de la loi de comportement.
