La loi fondamentale
La Loi Fondamentale ou Principe Fondamental de la Dynamique gouverne le mouvement des systèmes matériels en fonction des actions (forces, efforts,...) qui leur sont appliquées. Complétée à la fin du siècle dernier par les Equations de Maxwell elle est la base de la Physique Classique qui régnait avant les deux grandes révolutions du début du XXe siècle : la (petite) révolution Relativiste puis la (grande) révolution Quantique.
Enoncé
Le torseur ===> des quantités d'accélération (ou torseur dynamique) est égal au torseur des efforts extérieurs.

La quantité d'accélération d'un point matériel est le produit de sa masse par son accélération. C'est aussi la dérivée temporelle de sa quantité de mouvement, produit de sa masse par sa vitesse.
Le torseur des quantités de mouvement, ou torseur cinétique, est de la même manière défini par
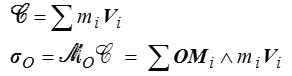
On démontre directement
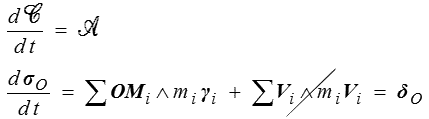
pour tout point O fixe. Le torseur dynamique est la dérivée par rapport au temps du torseur cinétique.
Origine
Pour le physicien, la loi fondamentale traduit l'homogénéité et l'isotropie de l'espace alors que le premier principe traduit, lui, l'homogénéité du temps.
- Homogénéité de l'espace
 Résultante
Résultante
- Isotropie de l'espace
 Moment
Moment
- Homogénéité du temps
 Premier Principe
Premier Principe
Dans une approche plus élémentaire, l'analyse mécanique d'un système de particules en interaction (>) en donne une compréhension fidèle, et notamment un premier aperçu de la notion d'efforts intérieurs, notion parfois ambiguë et source récurrente d'incompréhension en mécanique.
D'un point de vue mathématique, la loi fondamentale est une égalité entre torseurs, donc deux égalités entre vecteurs ou encore en revenant aux composantes :
- 6 relations scalaires dans le cas général tridimensionnel,
- 3 relations scalaires dans le cas bidimensionnel (résultante 2 + moment 1).
Théorème du centre d'inertie
Le centre d'inertie (ou de gravité, mais cette dernière terminologie est aujourd'hui déconseillée car elle entretient la confusion entre masse et poids) G d'un système mécanique est, de manière générale, défini par
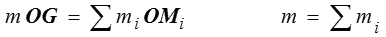
C'est un point géométrique, en général non matériel.
On en déduit alors directement en dérivant deux fois cette relation vectorielle

- La quantité de mouvement totale, résultante du torseur cinétique, est égale à la quantité de mouvement de la masse totale m concentrée en G.
- La résultante du torseur dynamique est égale à la quantité d'accélération de la masse totale m concentrée en G.
La partie résultante de la Loi fondamentale donne alors directement
Théorème du centre d'inertie.
Le centre d'inertie se comporte comme un point matériel de masse m (masse totale du système) soumis à la somme des forces (extérieures) appliquées au système.
C'est un thèorème important en mécanique car il justifie et autorise l'application du modèle de point matériel. (<)
Remarquons ici que les efforts en cause sont les efforts réellement appliqués au système, efforts extérieurs donc selon la terminologie consacrée. Les « efforts intérieurs » n'existent pas en soi. Vous pouvez pour l'instant les oublier en toute sérénité.
Théorème du moment cinétique
Pour écrire l'équation de moment de la Loi Fondamentale, il faut choisir un point. Ce point peut être quelconque et nous prendrons par exemple l'origine O du repère. On note δO et σO le moment dynamique et le moment cinétique en O respectivement. On démontre alors directement que le moment dynamique en O est la dérivée du moment cinétique en O. La partie moment de la Loi Fondamentale devient donc
Théorème du moment cinétique.
La dérivée du moment cinétique en O (point fixe) est égale au moment en O des efforts (extérieurs) appliqués au système.
Comme signalé plus haut, cette équation de moment peut être écrite en n'importe quel point, fixe ou non, mais le fait qu'il soit fixe permet de calculer le moment dynamique par dérivation du moment cinétique, sinon il faut s'y prendre autrement et ce sera plus compliqué !!!. Il y a toutefois une exception notable et très importante : le centre d'inertie G n'est en général pas fixe et pourtant :
Théorème.
Le moment dynamique en G est la dérivée du moment cinétique en G.
Il en résulte une variante du Théorème du moment cinétique :
Théorème du moment cinétique en G.
La dérivée du moment cinétique en G est égale au moment en G des efforts appliqués au système.
Remarquons enfin que ces subtilités, essentielles en Mécanique des Solides indéformables, ne joueront de fait aucun rôle en Mécanique des Milieux Continus. Ces résultats sont cependant généraux, que le système soit ou non déformable, et c'est pour cette raison qu'ils ont été donnés ici.
