Principe hamiltonien
Principe de moindre action
Nous avons évoqué plus haut l'approche alternative que constituait l'utilisation du principe des puissances virtuelles comme fondement de la Mécanique. Plus révolutionnaire encore est l'utilisation du principe de moindre action ou principe variationnel hamiltonien. (Attention, la terminologie est un peu trompeuse. Il ne faut pas confondre avec le formalisme hamiltonien (>) développé en Mécanique Analytique ; dans ce contexte le principe de moindre action est en fait à la base du formalisme lagrangien).
Cette approche consiste à affirmer comme principe premier que la solution u(t) d'un problème de mécanique (nous ne précisons pas davantage pour l'instant, la nature précise de cette fonction dépendra bien sûr du contexte) réalise le minimum − ou tout au moins un extremum − d'une quantité appelée « intégrale d'action »
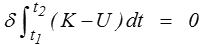
parmi l'ensemble de toutes les fonctions u(t) prenant aux instants t1 et t2 arbitrairement fixés une valeur donnée. Dans cette écriture δ représente la variation d'une quantité lorsque l'on rajoute à la fonction u(t) une variation infiniment petite δu(t) nulle en t1 et t2 (δu(t1) = δu(t2) = 0).
Nous avons déjà rencontré l'énergie cinétique K, et U désigne une « énergie potentielle » dont nous verrons plus loin l'interprétation.
Les équations de Lagrange
Considérons un système discret dont la configuration est à chaque instant définie par la valeur d'un nombre fini de paramètres q(t) (coordonnées généralisées).
C'est une situation très courante qui peut correspondre à un problème discret par nature :
- Point matériel défini par sa position x(t), (<),
- Système de N points matériels définis (3N paramètres), (>)
- Solide rigide dont la position est définie par 6 paramètres, (>)
- Système de solides rigides,
mais qui peut aussi correspondre à l'approximation d'un système continu discrétisé (par exemple par la méthode des éléments finis).
Dans ce cas l'énergie cinétique est une forme quadratique par rapport à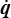 
, pouvant également dépendre de q, tandis que l'énergie potentielle ne dépend que de q.
Le calcul des variations permet alors d'obtenir l'équation du mouvement sous la forme
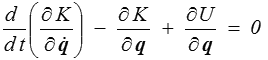
Ce sont les fameuses équations de Lagrange.
Esquisse de démonstration
C'est un problème classique en calcul des variations.
L'idée générale de sa résolution est la suivante.
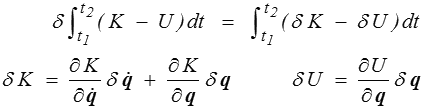
Comme toujours dans ce genre de situation, il faut se ramener à une équation
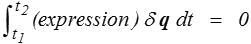
Ceci devant être vrai pour tout t1, t2 et toute variation δq, on en conclura naturellement que l'expression est nulle, ce qui nous donnera l'équation du mouvement.
Dans ce contexte, seul le terme en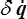 
pose problème, et on va donc l'intégrer par parties
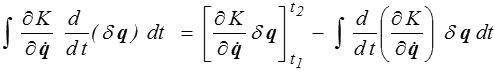
Le terme intégré disparaît puisque δq est nul en t1 et t2. Nous sommes arrivés à nos fins et il suffit maintenant de regrouper tous les termes
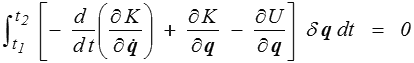
d'où la conclusion.
Le cas du point matériel
Le cas du point matériel va nous permettre de mieux cerner la signification de cette approche, et en particulier de ce que représente l'énergie potentielle. Dans ce cas en effet l'énergie cinétique est
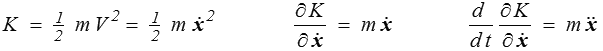
de sorte que l'équation de Lagrange se réduit à
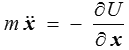
qui redonne l'équation du mouvement avec une force − ∂U / ∂x. On parlera alors d'une force « dérivant d'un potentiel » ou bien d'un « système conservatif ». Nous expliquerons cette terminologie plus loin, mais on peut déjà remarquer que ce sera le cas pour
- la force de pesanteur
f = m g U = − m g . x = m g z ( z verticale ascendante ) - la force de gravité (ou électromagnétique)
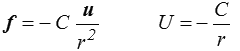
- la force exercée par un ressort
f = − k (r−lo ) u U = ½ k (r−lo )2
où l'on a noté u le vecteur unitaire porté par le vecteur OM
OM = x = r u r = | x | u = x / r
Cela ne sera par contre pas vérifié pour une force dépendant des vitesses f (V ), par exemple
- f = − k V / V frottement sec,
- f = − η V frottement visqueux,
- f = − c |V | V résistance de l'air.
Systèmes conservatifs
Plus généralement, un système obéissant au principe de moindre action tel que nous l'avons formulé, et donc aux équations de Lagrange, sera dit conservatif. Cette terminologie est justifiée par le théorème suivant
Théorème.
Dans un système conservatif K + U = Cte .
Il y a conservation de l'« énergie totale » (cinétique + potentielle).
La démonstration s'obtient en faisant le produit de l'équation de Lagrange par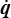
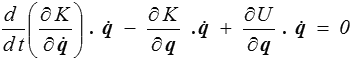
Puisque U ne dépend que de q, le dernier terme est la dérivée de U par rapport au temps. Les deux premiers termes, qui font intervenir l'énergie cinétique, peuvent aussi s'écrire
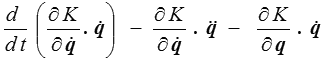
Pour le premier terme de cette expression, on remarque que, l'énergie cinétique étant fonction homogène de degré 2 par rapport aux vitesses, le théorème d'Euler donne
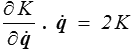
tandis que les termes restants donnent la dérivée par rapport au temps de K, fonction de q et .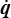
On obtient donc finalement
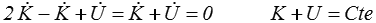
Dans un système conservatif l'énergie se conserve, ce qui de fait exclut la notion de dissipation. C'est là la limitation essentielle de cette approche. Il existe bien des approches permettant d'y réintroduire une certaine forme de dissipation, mais on perd du même coup la simplicité, la concision et l'élégance de cette approche alternative. Nous y renonçons donc en mécanique des milieux continus, car elle nous restreindrait alors au cas élastique.
Vers la Mécanique analytique ===>
Comme évoqué en introduction, on aura soin de ne pas confondre ce formalisme lagrangien avec le formalisme hamiltonien peu utilisé dans les applications courantes mais extrêmement important pour certains développements théoriques, notamment en physique statistique. Il est donc intéressant de l'évoquer rapidement, même si l'on sort ainsi du cadre strict de ce cours