Méthodes variationnelles
Les méthodes variationnelles que nous introduisons ici dans le cadre de la MMC bi- ou tri-dimensionnelle sont de portée très générale. Elles sont en fait l'outil de base pour traiter les problèmes d'équations aux dérivées partielles.
Cadre structurel ==>>
Elles s'appuient sur la dualité effort-mouvement, schématisée par le diagramme suivant
On introduit alors, pour un problème régulier, la notion de CCA (champ cinématiquement admissible) et de CSA (champ statiquement admissible), qu'il faudra ensuite mettre en correspondance par la loi de comportement.
Le théorème de l'énergie potentielle ==>>
La solution d'un problème régulier peut alors s'obtenir en minimisant, dans l'ensemble des CCA, une quantité scalaire, l'énergie potentielle définie par
U (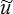 
i ) = W ( 
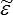ij ) − Tf d( 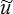i )
où W est l'énergie élastique et Tf d le travail des forces données pour le CCA 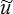i.
Le théorème de l'énergie complémentaire ==>>
De manière symétrique, on peut également trouver la solution en minimisant dans l'espace des CSA l'énergie complémentaire
( 
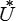ij ) = W ( ij ) − Tu d( ij )
où W est encore l'énergie élastique tandis que Tu d représente le travail dans les déplacements donnés pour le CSA ij.
Théorèmes de l'énergie ==>>
Le théorème du travail permet d'affirmer que pour la solution, le travail des efforts extérieurs (donnés) dans le déplacement solution est égal à deux fois l'énergie élastique
Tf d ( ui ) + Tud ( σij ) = 2 W
Il en résulte que pour la solution, l'énergie potentielle est opposée à l'énergie complémentaire. Les deux théorèmes variationnels, énergie potentielle et énergie complémentaire, se combinent alors pour donner le théorème de comparaison
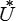− (ij ) ≤ − 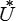( σij ) = U ( ui ) ≤ U ( 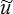i )
Ce théorème permet d'obtenir, à partir de tout CSA et de tout CCA, un encadrement de la solution.
On peut également, pour être complet, démontrer deux autres théorèmes, le théorème de Maxwell-Betti et le théorème de Castigliano, peu utilisés en MMC, mais très utiles pour d'autres modèles de structure et notamment en Résistance des Matériaux.
La méthode des éléments finis ==>>
Les théorèmes variationnels permettent aussi, et c'est sans doute là leur application la plus importante, de construire des solutions approchées, en « discrétisant » l'espace des CCA ou des CSA, c'est-à-dire en l'approchant par un ensemble dépendant d'un nombre fini de paramètres. Appliquée au théorème de l'énergie potentielle et en discrétisant l'espace des CCA, cela conduit aux méthodes d'éléments finis qui se sont imposées comme un standard pour la résolution des problèmes industriels.