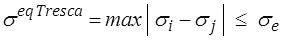Limite d'élasticité
Le modèle élastique que nous venons de présenter est très fréquemment utilisé. Si cette utilisation est très souvent légitime, il faut néanmoins conserver présent à l'esprit que, quel que soit le matériau utilisé, son domaine d'application est limité au domaine élastique. Nous avons déjà insisté sur le fait que tout calcul élastique devait s'accompagner de la vérification a posteriori de sa validité par un critère de limite d'élasticité.
Ce critère est usuellement écrit comme une condition portant sur les contraintes. C'est assez naturel, mais pour l'instant conventionnel puisque, en élasticité, contraintes et déformations sont liées ; on pourrait donc aussi bien l'écrire en fonction des déformations.
Contraintes normale et tangentielle
Les mécanismes physiques qui contrôlent cette perte d'élasticité peuvent être extrêmement divers. Leur conséquence macroscopique, ce qu'est en fait le critère de limite d'élasticité, reflète cette diversité et justifie une étude spécifique que nous repoussons au cours de Comportement des Matériaux ; nous nous limiterons, dans ce cours d'introduction, à une approche très élémentaire.
Dans une première approche, très simpliste, cette perte d'élasticité peut correspondre à
- une rupture par perte de cohésion, c'est ce qui se passe dans les matériaux fragiles, comme la craie. La physique et le bon sens suggèrent alors que ce sont les contraintes normales qui piloteront cette rupture.
- l'apparition de déformations irréversibles, comme dans les matériaux métalliques. La physique nous dit alors (Loi de Schmid) que ce sont les contraintes tangentielles qui contrôlent la mise en mouvement des dislocations, responsables de ces déformations irréversibles.
Rankine et Tresca
Deux critères très naturels consistent donc à écrire que l'on quittera le domaine élastique lorsque la contrainte normale Tn , dans le premier cas, et la contrainte tangentielle (ou plutôt sa norme, puisque c'est un vecteur), dans le second, atteindront une valeur critique.
Critère de Rankine.
Tn < Tncritique = σe
Critère de Tresca.
|Tt | < Ttcritique = ½ σe
où l'on a introduit la limite élastique en traction simple σe (on a vu (<) que la contrainte tangentielle maximale était, en général,
|Tt |max = ½ ( σ1 − σ3 )
si σ1 > σ2 > σ3 sont les trois contraintes principales et vaut donc ½ σe en traction simple).
Application à la torsion
Nous avons construit plus haut (<) une solution du problème de torsion d'un barreau cylindrique. Cette solution est générale pour le déplacement, mais nous avons insisté sur le fait que le champ de contrainte obtenu ne convenait que dans le cas d'une relation linéaire entre contraintes et déformations, donc justement dans le cas élastique qui nous intéresse ici. Nous avons en fait construit la solution (nous reviendrons plus loin sur le « la ») élastique du problème de torsion
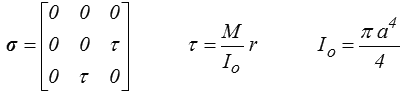
La contrainte est proportionnelle à r et sa valeur maximale sera atteinte à la périphérie r = a et vaudra
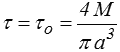
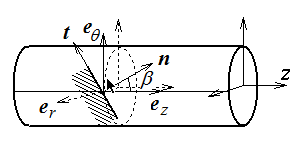Nous nous plaçons donc en un point de la périphérie et nous travaillons dans le repère local ( er , eθ , ez ). Considérons le vecteur contrainte qui s'exercera sur une facette inclinée de β par rapport à ez (facette dans le plan ( er , t ), interne au matériau bien sûr). L'évolution des contraintes, lorsque β varie, est directement donnée par le cercle de Mohr (<) et, en cas de besoin, je renvoie le lecteur sur l'animation que nous avons alors présentée.
Pour un matériau métallique la plastification, puis rupture, se produiront pour la contrainte tangentielle maximale, donc pour β = 0 (ou β = π / 2, mais ceci ne correspond pas à un mode de rupture global).
Pour un matériau fragile la rupture se produira pour la contrainte normale maximale, soit pour β = π / 4. C'est bien ce que confirme l'expérience réalisée sur une éprouvette métallique d'une part, sur un bâton de craie d'autre part.
Critère de von Mises
Pour un matériau métallique donc, ce sont les contraintes tangentielles qui pilotent l'entrée en plasticité (c'est-à-dire l'apparition de déformations plastiques irréversibles, qui résultent elles-mêmes du mouvement irréversible des dislocations). Or ces contraintes tangentielles ne dépendent que du déviateur des contraintes. Pour un matériau métallique le critère de limite d'élasticité ne fera intervenir que le déviateur des contraintes
f ( sij ) ≤ 0
Et, effectivement, on peut vérifier expérimentalement qu'une pression hydrostatique, même très forte, n'entraîne pas de plastification.
Le critère le plus simple consiste alors à dire que la plasticité apparaît lorsque l'« intensité » du déviateur atteint une valeur critique, et tout naturellement nous mesurons cette intensité par la norme euclidienne du déviateur (c'est-à-dire par la somme des carrés des composantes)
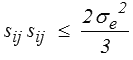
puisque dans un essai de traction simple
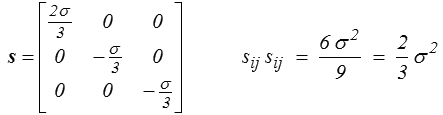
En termes géométriques, le domaine élastique est une boule de rayon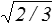 
σe dans l'espace des déviateurs.
C'est le critère qui est le plus classiquement utilisé pour les matériaux métalliques. Il est en fait assez proche du critère de Tresca. Nous reviendrons sur ces deux critères dans le cours de Comportement, mais j'invite le lecteur à retenir pour l'instant que ces deux critères traduisent la même réalité physique d'un matériau métallique, et que l'on choisira l'un ou l'autre en fonction des circonstances (typiquement, on utilisera en général von Mises, sauf lorsque l'on connaîtra a priori les directions principales, auquel cas le critère de Tresca peut être plus sympathique).
Cette présentation du critère de von Mises comme limite de la norme du déviateur est, à mon avis, la plus physique. Toutefois certains ont pu la trouver un peu abstraite et ont cherché à en donner une vision à leurs yeux plus « concrète ».
Par exemple, on peut dire que le critère de von Mises limite la part d'énergie élastique provenant du déviateur, laquelle est, comme nous l'avons vu (<), justement donnée par
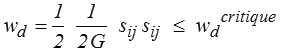
Contraintes octaédriques
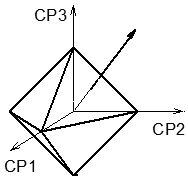Une autre interprétation, tout aussi artificielle à mon avis, mais néanmoins très instructive, est basée sur la notion de contraintes octaédriques. On appelle ainsi les contraintes appliquées sur les 8 facettes correspondant aux trissectrices du repère principal des contraintes (ces 8 facettes, représentées ci-contre, forment un octaèdre, d'où la terminologie).
Dans le repère principal
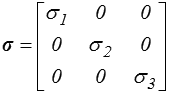
et la facette correspondant, par exemple, au premier quadrant est définie par n 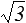= ( 1 /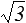
, 1 /, 1 /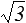 ). Le vecteur contrainte est alors
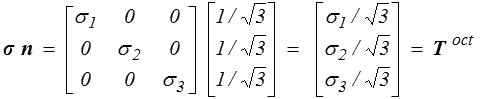
La contrainte normale s'obtient en projetant sur n
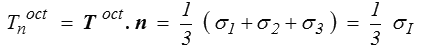
Ainsi la contrainte normale octaédrique est égale à la contrainte moyenne σI / 3.
La contrainte tangentielle s'obtient de même comme
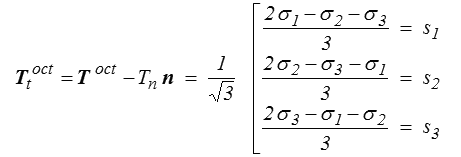
et l'on reconnaît les composantes principales s1, s2 et s3 du déviateur. Sa norme est bien sûr
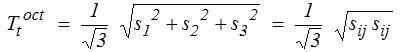
Ainsi, on peut interpréter le critère de von Mises comme limitant la contrainte tangentielle octaédrique, considérée comme représentative des contraintes tangentielles.
Au delà de l'anecdote, cela montre bien que la partie sphérique et la norme du déviateur sont deux grandeurs représentatives des contraintes normale et tangentielle au point considéré.
Contrainte équivalente de von Mises
Il est usuel de réécrire le critère de von Mises (<) sous la forme
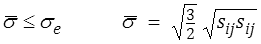
où la quantité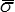 
ainsi définie est appelée contrainte équivalente de von Mises (voire même contrainte équivalente tout court) : cette formule permet de traduire un état de contrainte complexe en une contrainte de traction qui lui est − vis-à-vis du critère de von Mises − équivalente. On devrait en fait parler d'une contrainte de traction équivalente.
D'un point de vue pratique, c'est, pour un matériau métallique, le résultat le plus direct d'un calcul éléments finis. Une cartographie de cette contrainte équivalente permet en effet de repérer le point le plus sollicité puis d'évaluer, par comparaison de la valeur maximale à la limite élastique en traction, la capacité de résistance de la structure considérée.
On pourrait de même définir une contrainte équivalente de Tresca
