Cercle de Mohr
Définition & Démonstration
On considère un état de contrainte bidimensionnel et une facette de normale n.
La direction tangentielle t est choisie orientée à + π/2 de n.
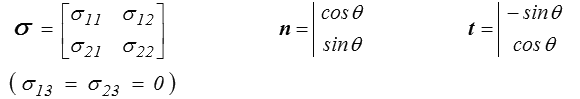
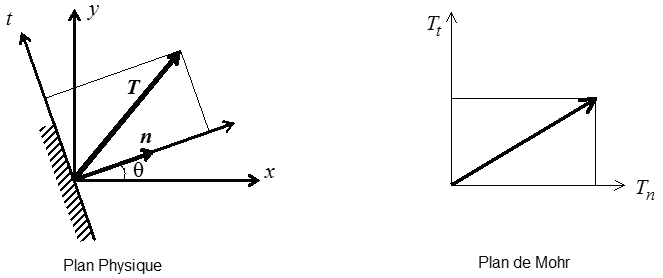
Le vecteur contrainte T associé à cette facette est donc, dans le repère (x, y) (plan physique),
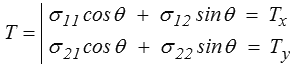
puis, dans le repère (n, t) (plan de Mohr),
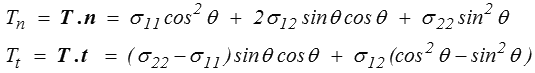
soit, en réarrangeant les termes,
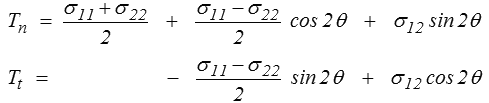
Le cercle de Mohr
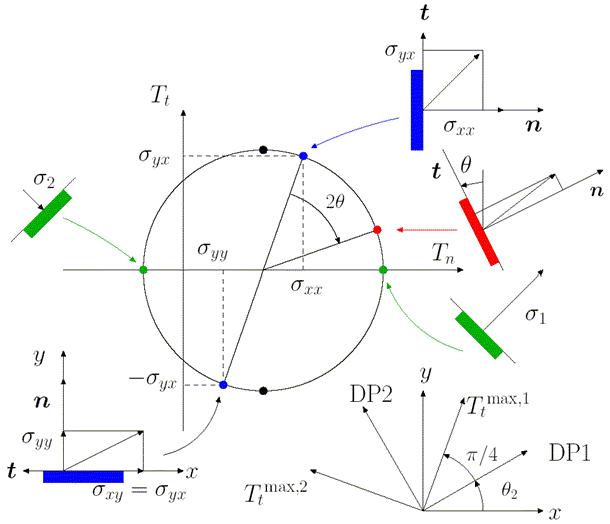
Dans le plan (Tn , Tt ) le point correspondant décrit, lorsque θ varie, le cercle de Mohr :

Construction & Utilisation
A partir des composantes du tenseur des contraintes on construira le Cercle de Mohr à partir des 2 points bleus.
- Facette normale à l'axe x1 : Tn = σ11 , Tt = σ12.
- Facette normale à l'axe x2 : Tn = σ22 , Tt = − σ12.
On pourra alors déterminer simplement le point courant rouge par rotation de − 2θ dans le plan de Mohr, pour une rotation de + θ dans le plan physique, et donc en particulier : - Les directions et contraintes principales (points verts).
- Les directions correspondant aux contraintes tangentielles maximales (points noirs).
Animation
Cette animation permet de visualiser, dans le plan physique et dans le plan de Mohr, l'évolution du vecteur contrainte lorsque la facette tourne. Vous pouvez la télécharger et vous trouverez ici comment l'utiliser
Je vous conseille de tester divers états de contrainte, de figer l'animation pour bien comprendre ce qui se passe, puis d'essayer de prévoir le résultat avant de lancer.
