Travaux virtuels - Déformations
Théorème des Puissances Virtuelles ==>>
Contrairement à la notion d'efforts intérieurs, notion floue car dépendant de la décomposition du système considéré en sous-systèmes, leur puissance est, elle, parfaitement définie par le Théorème des Puissances Virtuelles. Or en Mécanique des Milieux Continus
- La puissance virtuelle des quantités d'accélération résulte simplement de la description du mouvement (<),
- La puissance virtuelle des efforts extérieurs découle de leur description et du postulat de Cauchy (<).
La puissance des efforts intérieurs sera alors directement donnée par leur différence, et un calcul direct conduit ainsi à l'expression suivante

Cette expression introduit le tenseur des Taux de Déformations Dij. Ce tenseur s'annule dans un mouvement rigidifiant et on retrouve donc bien une puissance virtuelle des efforts intérieurs nulle dans tout mouvement rigidifiant.
En mécanique des solides HPP on préfère souvent aux puissances virtuelles les travaux virtuels. Ceci conduit naturellement au tenseur des déformations
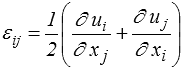
Description des déformations ==>>
Et, effectivement, ces quantités εij permettent de caractériser les « déformations », c'est-à-dire les allongements ε (variations de longueur) et les glissements γ (variations d'angle) pour toutes les directions
ε(n) = εij ni nj γ(m, n) = 2 εij ni mj
Le tenseur des déformations ==>>
Ces quantités définissent donc le tenseur des déformations infinitésimales pour lequel on peut, comme pour le tenseur des contraintes (<),
- Interpréter les composantes
- sur la diagonale : allongements,
- en dehors de la diagonale : glissements.
- Diagonaliser et introduire les allongements principaux.
- Décomposer en partie sphérique et déviateur.
- Etablir les formules de changement de repère.
- etc.....
Représentations Géométriques ==>>
Comme pour les contraintes (<) on peut introduire l'ellipsoïde de Lamé, la quadrique directrice des déformations, la représentation de Mohr, etc... Ces représentations perdent toutefois beaucoup de leur signification physique.
Dans le cas plan toutefois, on peut redonner tout son sens à la représentation de Mohr en introduisant le Cercle de Mohr des transformations.
Compatibilité des déformations ==>>
Les déformations s'obtiennent par dérivation du champ de déplacement. Réciproquement en partant des déformations on peut tenter d'« intégrer » les déplacements. Pour pouvoir le faire il faut que les déformations vérifient 6 équations différentielles du second ordre : les équations de compatibilité.
Si tel est le cas, alors on pourra calculer le champ de déplacement à un mouvement de solide rigide près.
