Compatibilité des déformations
Intégration des déplacements
Les déformations s'obtiennent par dérivation des déplacements
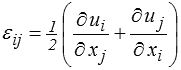
Réciproquement, comment peut-on calculer les déplacements à partir des déformations (nous verrons plus loin l'intérêt ou la nécessité de ce type de calcul) ? Partant d'un champ de déformation εij(x), il faut, pour calculer le déplacement ui(x), intégrer ce système d'équations aux dérivées partielles.
D'un point de vue mathématique, il s'agit d'un système linéaire non homogène. Sa solution générale est donc la somme d'une solution particulière de l'équation complète et de la solution générale de l'équation homogène
ui (x) = uio(x) + uiR(x)
uio : une solution particulière,
uiR : la solution générale de l'équation homogène (la notation R trouvera très bientôt son explication).
Solution de l'équation homogène
Partant de la décomposition du gradient de déplacement en parties symétrique et antisymétrique
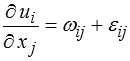
et en utilisant la définition de εij, on obtient facilement
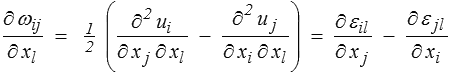
Cette dérivée est donc nulle pour le problème homogène (εij = 0). La rotation est donc constante
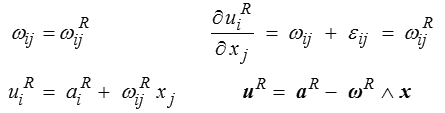
en introduisant le vecteur ωR adjoint de ωijR. On retrouve bien le mouvement de solide rigide que l'on attendait. L'intégration des déplacements à partir des déformations définira le champ de déplacement à un déplacement de solide rigide près.
Equations de compatibilité
Théorème.
Une CNS pour que l'on puisse intégrer les déplacements est que soient vérifiées 6 équations
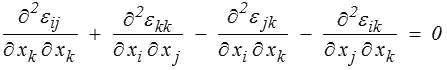
Ce sont les « équations de compatibilité ».
Sans être très difficile la démonstration en est un peu technique, et nous renvoyons le lecteur intéressé au polycopié (§ III-3, pp.24-27) où l'on trouvera également d'autres formes de ces équations. Plus que leur forme précise, auxquelles on pourra se référer en cas de besoin, il importe de conserver à l'esprit leur rôle :
- si elles ne sont pas vérifiées, il n'existe pas de champ de déplacement compatible avec ces déformations (d'où la terminologie « compatibilité des déformations »).
- Si elles sont vérifiées alors on peut déterminer ce champ, à un déplacement de solide rigide près.
Un cas particulier
Ces équations sont des équations aux dérivées partielles du second ordre. Elles seront donc automatiquement vérifiées pour un champ de déformation polynômial du premier ordre
εij = Aijk xk + εijo
où les Aijk et εijo sont des quantités constantes (6 pour εijo et 18 pour Aijk). Pour calculer le déplacement correspondant, on part de l'expression obtenue plus haut
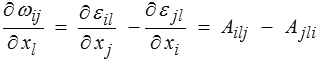
qui, par intégration, donne
ωij = (Ailj − Ajli ) xl + ωijo
On en tire ensuite
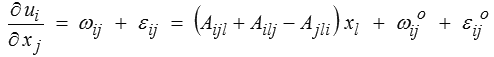
et en intégrant une seconde fois
ui = (Aijk + Aikj − Ajki ) xj xk /2 + εijo xj + ωijo xj + uio
Sans être insurmontable, ce calcul montre bien la difficulté - même dans un cas très simple - de cette intégration des déplacements. C'est aussi un bon exercice de manipulation des notations indicielles, et je vous invite à bien le maîtriser.
