Réservoirs sphériques
Solution en symétrie sphérique
Pour résoudre le problème du réservoir sphérique, nous allons étudier la solution générale des équations de l'élasticité (loi de Hooke) pour un problème à symétrie sphérique. On peut alors affirmer que le déplacement est radial et ne dépend que du rayon r
ur = u ( r ) uθ = uφ = 0
Cette hypothèse permet d'enclencher le schéma général de solution (<) à partir du déplacement. En l'absence de conditions cinématiques, nous devons ensuite calculer les déformations. Nous nous reportons pour cela au formulaire de MMC en coordonnées sphériques (<) qui, combiné à la loi de Hooke, donne
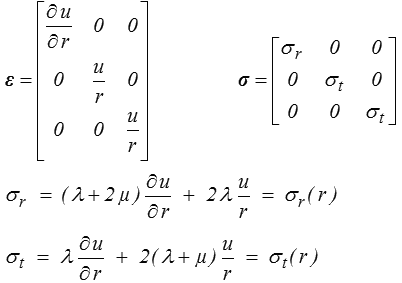
Il suffit alors de reporter dans les équations d'équilibre (<) qui, en l'absence de forces de volume, se réduisent à
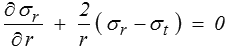
et il suffit de substituer l'expression des contraintes en fonction de u pour obtenir l'équation différentielle du second ordre qui permet de calculer la fonction u ( r ). Je laisse au lecteur patient le soin de mener ce calcul, mais on peut en fait s'en dispenser. En effet, dans ce cas particulier, les équations de Navier vont nous donner directement le résultat. Le rotationnel du champ u est en effet nul, et les équations de Navier nous donnent directement
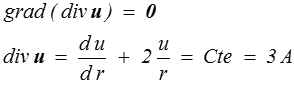
Il suffit alors d'intégrer cette équation, par exemple en la multipliant par r 2
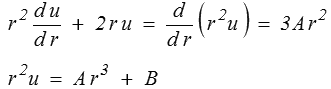
de sorte que finalement
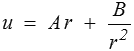
solution générale des équations de l'élasticité de Hooke en symétrie sphérique. Cette solution fait intervenir deux constantes d'intégration A et B.
Calcul des contraintes
Les contraintes ont déjà été calculées, mais la solution obtenue pour u va nous suggérer une forme plus simple. En effet, les déformations sont
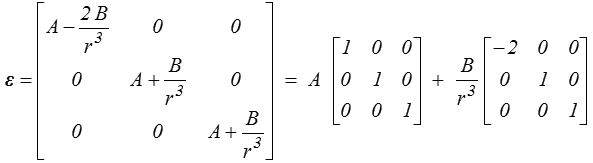
ce qui correspond à la décomposition du tenseur des déformations en partie sphérique et déviateur. Or nous avons vu que, dans cette décomposition, la loi de Hooke se ramenait à deux lois scalaires indépendantes (<). Nous écrirons donc
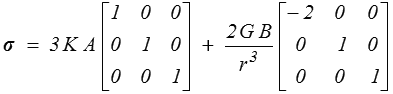
soit, pour σr et σt ,
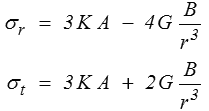
En coordonnées cartésiennes
Nous avons utilisé, pour mener les calculs, les coordonnées sphériques. C'est bien naturel, mais nous aurions tout aussi bien pu travailler sans formulaire et en coordonnées cartésiennes. Le champ radial u = u ( r ) peut en effet s'écrire
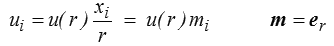
où er = m est le vecteur unitaire dans la direction radiale.
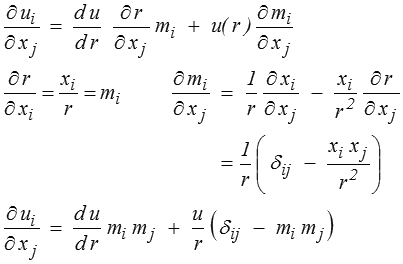
On remarque au passage que ce tenseur est symétrique, le rotationnel de u est donc bien nul, et nous obtenons, pour la déformation, le résultat obtenu plus haut avec comme déformation principale ∂ u / ∂ r dans la direction radiale et u / r dans les deux directions perpendiculaires. La dilatation εI = εii = div u est donc
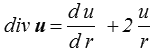
ce qui permet, comme plus haut, de trouver la forme de u à partir des équations de Navier. Le formulaire en coordonnées sphériques est indispensable pour traiter des problèmes plus complexes, mais on peut ici s'en passer.
Le réservoir sphérique sous pression
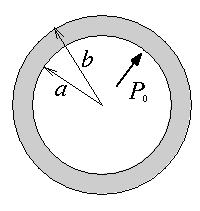Reste à déterminer les deux constantes d'intégration A et B, ce que permettront les conditions aux limites. Pour le réservoir sous pression (<) par exemple, ces conditions s'écrivent
r = a σr = − Po
r = b σr = 0
ce qui donne
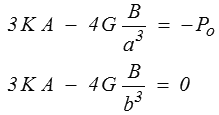
soit, par résolution,
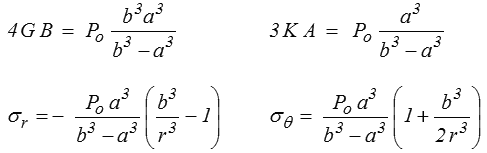
La contrainte σr varie, comme l'on pouvait s'y attendre, entre − Po ( r = a ) et 0 ( r = b ), tandis que la contrainte σθ est positive, ce qui correspond à une tension.
Pour un réservoir métallique on remarque que le déviateur est
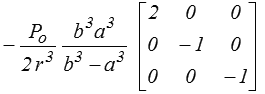
forme identique à celle que nous avons obtenue en traction simple, si l'on pose
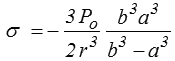
Le critère de Tresca ou de von Mises s'écrira donc en tout point
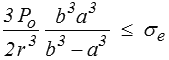
La valeur la plus élevée est atteinte à l'intérieur, pour r = a, et la condition de résistance s'écrira donc
Cette condition permet de dimensionner le réservoir, c'est-à-dire de déterminer l'épaisseur nécessaire pour résister à une pression donnée. On constate toutefois qu'un réservoir sphérique ne pourra jamais résister à une pression intérieure supérieure à 2 σe / 3.
Laissons au lecteur méticuleux le soin d'écrire le critère de Rankine, mais il ne viendrait, j'espère, à l'esprit de personne de construire un tel réservoir avec un matériau fragile.
Deux cas limites
Lorsque b devient très grand, on obtient en première approximation
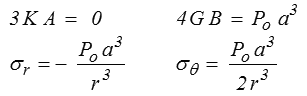
Cette solution correspond à une cavité sphérique sous pression dans un massif infini, problème important dans les sols et là, le cas d'un matériau fragile peut prendre toute son importance.
Dans le cas d'un réservoir mince (l'épaisseur e = b − a est petite devant le rayon) la contrainte radiale σr varie toujours entre 0 et − Po , tandis que la contrainte circonférentielle vaut en première approximation ( b / r ~ 1)
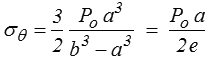
Elle est donc grande par rapport à la contrainte radiale qui peut alors être négligée, et on écrira en première approximation
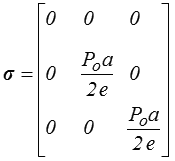
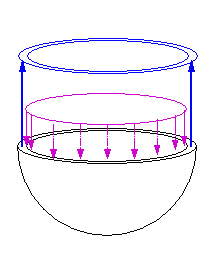résultat que l'on peut d'ailleurs obtenir en écrivant l'équilibre d'une demi-sphère (enveloppe + gaz) : la contrainte circonférentielle σθ appliquée sur la couronne de rayon a et d'épaisseur e devant équilibrer la pression Po appliquée sur le cercle de rayon a
2 π a e σθ = π a 2 Po
On remarquera que ce résultat est basé sur les seules équations d'équilibre. Il ne dépend donc pas de la loi de comportement, contrairement à ce que nous avons fait au préalable.
Autres problèmes
La solution générale que nous avons construite peut également s'appliquer pour traiter d'autres problèmes à symétrie sphérique.
Nous avons déjà traité, par passage à la limite b 
∞, le cas d'une cavité sphérique dans un massif infini.
Le cas d'une enveloppe sphérique soumise à une pression externe P1 se traiterait exactement de la même manière et donne comme solution
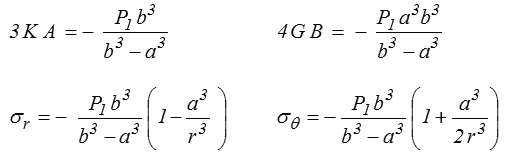
Remarquons simplement que là encore, et contrairement à ce que certains auraient pu attendre, les points les plus sollicités seront toujours à l'intérieur r = a.
Si maintenant le réservoir est soumis à une pression externe P1 et une pression interne Po , il suffit de superposer les deux solutions (principe de superposition, toujours valable dans une théorie linéaire).
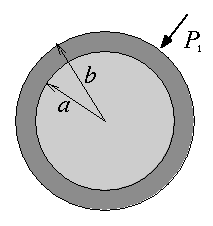Considérons maintenant le cas d'une boule composite constituée de deux matériaux 1 et 2 et soumise à une pression externe P1. La solution aura, dans chaque matériau, la forme générale obtenue plus haut, avec toutefois des constantes différentes
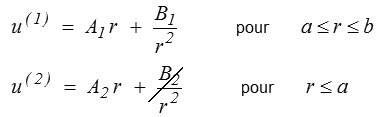
puisque B2 doit disparaître pour éviter une singularité à l'origine. Cette solution fait intervenir trois constantes d'intégration que l'on déterminera en écrivant
- la condition de pression en r = a,
- les conditions de raccord pour u et σr en r = b.
Attention : la contrainte circonférentielle σt sera en général discontinue (<). On pourrait traiter de manière analogue tout assemblage composite de ce type.
On rencontrera également cette solution de base pour l'étude des contraintes thermiques susceptibles d'apparaître, par exemple lors de traitements thermiques.
Contraintes à symétrie sphérique
Nous avons choisi d'exploiter la symétrie sphérique sur le vecteur déplacement ; c'était bien naturel, mais il peut être instructif de l'exploiter directement sur les contraintes. La symétrie sphérique se traduit alors par la forme suivante
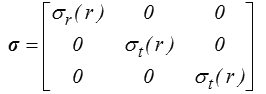
et les équations d'équilibre (<) se ramènent à la seule équation
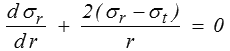
équation d'équilibre qui, pour résoudre le problème, devra être complétée par une équation provenant de la loi de comportement. En bonne logique ce devrait être les équations de Beltrami, mais elles sont − sans doute, je ne me rappelle pas les avoir jamais écrites − assez compliquées en coordonnées sphériques. Il va être plus commode de décomposer σ en déviateur et partie sphérique
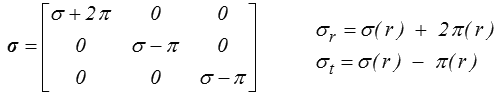
L'équation d'équilibre devient, avec ces nouvelles variables,
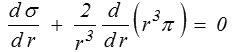
Cette équation est générale et applicable à n'importe quelle loi de comportement. Pour l'élasticité de Hooke, la manière la plus simple est d'utiliser, comme plus haut, l'équation de Navier qui nous donne εI = Cte.
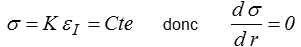
et l'équation d'équilibre se réduit à
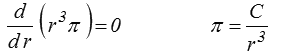
redonnant ainsi la solution obtenue plus haut.
Sommes-nous bien sûrs d'avoir ainsi construit la solution pour notre réservoir sphérique ? Qu'en pensez-vous ?
En première lecture, non car si les équations de Navier doivent être satisfaites, elles ne garantissent pas pour autant que les autres le sont aussi, et notamment qu'il existe un vecteur déplacement. Mais en y réfléchissant, oui quand même, en vertu du théorème d'existence qui nous garantit l'existence d'une solution unique ; nous avons montré que le champ de contrainte devait avoir cette forme, c'est donc la solution. A nouveau, pour trouver la solution, tous les moyens sont bons.