Introduction aux éléments finis
Méthodes de Ritz-Galerkin
En changeant la nature du problème et en ramenant un ensemble d'équations à une simple minimisation, les méthodes variationnelles engendrent naturellement des méthodes numériques d'approximation. Partant par exemple du Théorème de l'énergie potentielle, il suffit en effet de construire par combinaison linéaire un ensemble de champs cinématiquement admissibles
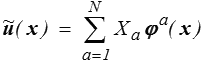
où nous avons, pour simplifier, supposé que les déplacements donnés étaient nuls, sinon il faudrait choisir un CCA u o(x) et travailler sur u − u o. Les φ a(x) sont des CCA de base choisis a priori, et leur combinaison linéaire sera également CCA. L'énergie potentielle de ce CCA sera alors
U ( 
) = W ( ) − Tfd( )
L'énergie élastique est quadratique en tandis que le travail est linéaire en ; on obtiendra donc en reportant
U ( ) = U ( X ) = ½ X T.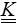 
X − F X
où X est le vecteur colonne des Xa, et où la matrice de rigidité 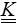et la force généralisée F sont définis par
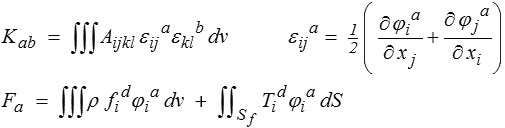
Chaque X donne une majoration de l'énergie potentielle solution, et la meilleure sera la plus petite. On choisira donc X pour minimiser U, donc en résolvant le système
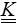X = F X = 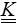−1 F
Sauf miracle, le CCA ainsi construit n'est pas solution, mais si les CCA de base ont été judicieusement choisis et suffisamment nombreux, on peut espérer une approximation raisonnable. C'est d'ailleurs ainsi que l'on peut démontrer l'existence d'une solution : on choisit pour φ a une « base » de l'espace des CCA et on peut alors montrer que, en un certain sens, l'approximation ainsi construite tend vers la solution du problème lorsque N 
∞. On parle alors de méthode de Galerkin ou de Ritz-Galerkin.
Bien évidemment nous pourrions développer une méthode analogue à partir du théorème de l'énergie complémentaire et en travaillant dans l'espace des CSA. Il est toutefois bien plus difficile de construire des CSA, et, malgré quelques tentatives, cela n'a guère débouché.
On utilise très préférentiellement en élasticité les « méthodes en déplacements » basées sur une discrétisation de l'espace des CCA.
Application
Si nous revenons à notre problème modèle, le CCA que nous avons construit (<) est une première étape dans cette direction. Il est facile d'élargir l'ensemble des CCA considérés en prenant par exemple
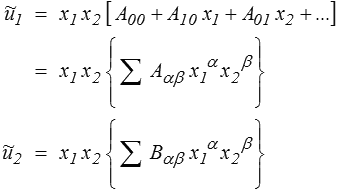
et l'on obtiendra ainsi des solutions approchées dont la qualité augmentera au fur et à mesure que l'on prendra davantage de termes en compte dans ce développement.
Les mathématiciens nous disent que l'on peut toujours approcher une fonction quelconque par un polynôme. Nous pouvons donc espérer que cette solution approchée tendra vers la solution exacte lorsque l'on poussera ce développement de plus en plus loin. C'est effectivement le cas!
Pour un domaine rectangulaire ou carré, on peut également développer la solution sur une base de sinus et cosinus, ce qui correspond au développement de la solution en série de Fourier.
Deux autres discrétisations
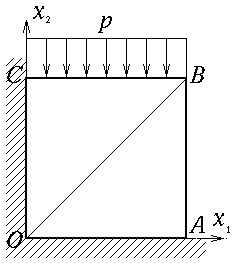Une autre possibilité, pour construire un CCA, consiste à décomposer le carré OABC en deux triangles OAB et OBC et de choisir un CCA linéaire sur chacun de ces deux triangles. On écrira donc simplement
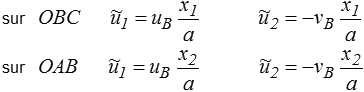
où ( uB ,− vB ) représente pour ce CCA le déplacement du coin B.
L'énergie élastique de ce CCA s'obtient en sommant la contribution des deux triangles, chacune se calculant très simplement car la déformation et donc la densité d'énergie de déformation y sont constantes. On obtient sur OBC
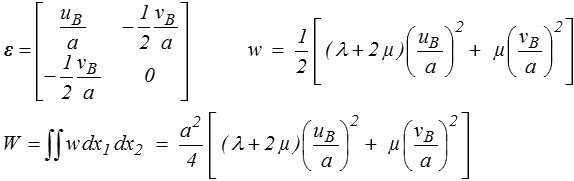
et de la même manière sur OAB
L'énergie élastique est donc
Le travail des efforts donnés sera de même
L'approximation correspondante sera donc
La valeur correspondante de l'énergie potentielle est
U ( ) = ½ X T. 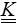X − F TX = −½ F TX si X = 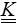−1F
donc ici
soit, en terme de rigidité (<),
k ≤ 8 μ ( si λ = μ , ν = 1/4 )
un résultat moins bon que celui obtenu plus haut, mais là n'est pas l'essentiel.
On peut également construire un CCA similaire à partir des deux triangles OAC et ABC. Il vient alors (nous laissons les détails au lecteur)
sur OAC 
1 = 2 = 0
et donc w = 0
sur ABC 
et donc par intégration
Le travail des forces données conduit au même résultat que plus haut et finalement
En supposant désormais, toujours pour simplifier les calculs, λ = μ, ν = 1/4
soit finalement
k ≤ 6 μ
un résultat meilleur que celui obtenu avec l'autre décomposition, mais toujours moins bon que celui construit auparavant.
Une discrétisation éléments finis
Pour aller plus loin on peut étendre la construction précédente en décomposant le domaine en un ensemble de triangles (32 sur le schéma présenté) et en cherchant un CCA linéaire sur chacun des triangles. Sur chaque triangle chaque composante du déplacement sera fonction linéaire de x1 et x2, et cette fonction sera complètement définie par sa valeur en trois points, par exemple, et c'est le plus simple, sa valeur aux trois sommets du triangle. Le CCA sera donc complètement défini par sa valeur aux 16 « nœuds » marqués d'un point gras (le déplacement est nul sur OA et OB), ce qui conduit à 32 variables, les « déplacements nodaux » (ici on a exactement autant de variables nodales que de triangles, c'est un accident, ces deux nombres sont toujours comparables mais indépendants l'un de l'autre).
Méthode d'éléments finis
Une méthode d'éléments finis est donc basée sur
- Un découpage du domaine d'étude en éléments simples (on parle de maillage).
- Le choix sur chaque élément d'une forme analytique simple déterminée par un nombre limité de variables nodales.
Il suffit ensuite de reporter dans le principe variationnel pour déterminer la valeur optimale de ces variables et donc une solution approchée. On peut espérer, et en effet cela se démontre, que l'on peut approcher la solution en diminuant la taille du maillage.
Nous avons introduit une première famille d'éléments : les « triangles à 3 nœuds » ou élément P1 (polygone de degré 1)
Deux autres types d'éléments sont fréquemment utilisés en mécanique (et dans bien d'autres domaines).
Les « triangles à 6 nœuds » ou élément P2 où chaque variable est un polynôme du second degré par rapport aux coordonnées (donc défini par sa valeur en 6 points, les sommets et les milieux des côtés). Une extension simple (éléments isoparamétriques) permet d'étendre les éléments P2 en triangles curvilignes (ce qui est bien évidemment très sympathique pour décrire une frontière courbe). En mécanique des solides ces éléments P2 sont souvent recommandés.
Les « rectangles à 4 nœuds » ou élément Q1 où chaque variable est un polynôme du 1er degré par rapport à chacune des coordonnées, et donc de la forme
a + b x1 + c x2 + d x1 x 2
défini par sa valeur aux 4 sommets du rectangle. Là encore les éléments isoparamétriques permettent d'étendre à un quadrilatère quelconque.
En fait, la première approximation discutée pour notre problème modèle (<)) correspond à une discrétisation par un seul élément Q1.
Ce type de méthode s'est imposé comme un standard en mécanique des solides, et plus généralement pour tout problème d'équations aux dérivées partielles. La raison principale en est que ce type de discrétisation peut s'appliquer à n'importe quelle géométrie et qu'elle est facilement informatisable, ce qui a permis le développement de codes industriels.
Nous n'insisterons pas davantage, renvoyant le lecteur vers les nombreuses ressources existantes.