Théorème de l'énergie complémentaire
Le théorème de l'énergie complémentaire joue pour les CSA un rôle symétrique au théorème de l'énergie potentielle pour les CCA. Nous travaillons donc sur des champs de contrainte et la loi de comportement s'écrira
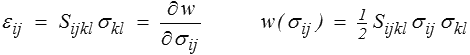
Rappelons qu'il s'agit en fait de la densité d'énergie complémentaire w c qui, en élasticité linéaire, se trouve être égale à l'énergie élastique exprimée en fonction des contraintes (<).
Energie complémentaire d'un CSA
Définition.
L'énergie complémentaire d'un CSA 
ij est
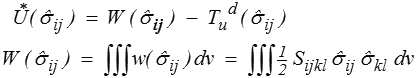
Et le théorème de l'énergie complémentaire permet de reconnaître la solution parmi tous les CSA ij
Théorème de l'énergie complémentaire.
Le champ solution σij( x) minimise l'énergie complémentaire parmi tous les CSA
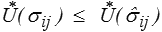
On peut ici faire des commentaires tout à fait symétriques de ceux faits à propos du théorème de l'énergie potentielle. En particulier, en se référant au second schéma de résolution (<) d'un problème régulier, les étapes 1 à 3 suffisent à définir un CSA et permettent, si l'on ne peut aller au bout de la démarche, d'obtenir une borne supérieure de l'énergie complémentaire de la solution.
Il sera, en général, d'utilisation plus rare, car les CSA doivent vérifier les équations d'équilibre et sont plus difficiles à imaginer.
Signalons aussi que l'on définit parfois l'énergie complémentaire comme l'opposé de celle que nous avons définie. C'est notamment ce que je fais dans le polycopié (poly ch IX) où j'utilisais la notation
K (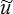 
i ) pour U ( 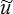i ) et H ( ij ) pour − 
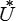( ij ).
Démonstration.
Elle est, au départ, analogue à celle du théorème de l'énergie potentielle : on pose
ij = σij + ijo
où le CSAo ijo vérifie les conditions homogènes
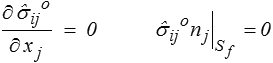
On obtient alors, de manière complètement analogue à ce que nous avons fait pour le théorème de l'énergie potentielle,
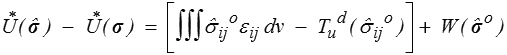
Comme précédemment, si le terme entre crochets est nul, alors
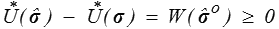
et la solution σ minimise l'énergie complémentaire. Or il est nul :
Lemme.
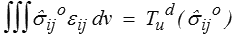
On démontre ce lemme en appliquant le lemme fondamental au problème auxiliaire défini par des forces de volume nulles et les conditions aux limites
σij nj |Sf = 0 ui |Su = uid
La solution ui du problème réel est évidemment CCA pour ce problème, tandis que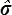 
o, CSAo, est statiquement admissible pour ce problème. Le lemme fondamental donne alors
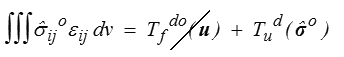
puisque pour ce problème auxiliaire les efforts donnés sont nuls.
Resterait à montrer la réciproque, c'est-à-dire que si σij minimise l'énergie complémentaire alors c'est la solution. Cette démonstration est nettement plus difficile, il faut, en particulier, vérifier que le champ de déformation εij déduit de σij par la loi de Hooke vérifie les équations de compatibilité (<). Sans présenter de difficultés insurmontables, cette démonstration est lourde et technique, et je la laisse de côté.
Application
Revenons à notre problème modèle (<). Pour pouvoir appliquer le théorème de l'énergie complémentaire, il nous faut trouver un CSA ij, c'est-à-dire un champ de contrainte vérifiant les équations d'équilibre et les conditions aux limites sur les faces AB et BC. C'est en général plus difficile, mais un champ de contrainte homogène (indépendant de x1 et x2) vérifiera toujours les équations d'équilibre. Les conditions aux limites en x1 = a et x2 = 0 donnent alors directement
11 = 12 = 0
22 = −po
Les déplacements donnés (sur OA et OB) sont nuls, de sorte que Tud = 0 et l'énergie complémentaire se réduit à l'énergie élastique. Pour calculer cette énergie élastique il est tentant de partir des formules donnant la densité d'énergie en fonction des contraintes pour écrire
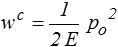
C'est faux.Pourquoi ?
Parce que nous sommes en déformation plane et la contrainte σ33 est non nulle. Il faut utiliser les formules adaptées à ce cadre (<).
En fait on a
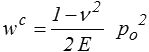
Soit finalement
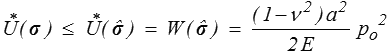
ou dans le cas particulier ν = 1/4 ( E = 5 μ/2 )
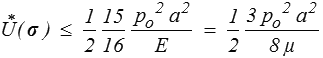
résultat garanti, mais qui, pour l'instant du moins, ne semble pas nous apporter grand-chose.