Loi Fondamentale - Contraintes
Dans le cadre de la Mécanique des Milieux Continus nous avons vu comment caractériser le mouvement, que l'on fasse (<), ou non (<), l'Hypothèse des Petites Perturbations. Nous savons donc définir le torseur des quantités d'accélération. Pour pouvoir écrire et utiliser la Loi Fondamentale, il nous faut maintenant caractériser les efforts appliqués sur un domaine matériel : efforts extérieurs ou intérieurs ? extérieurs bien sûr ; rappelons que la Mécanique ne connaît que ceux-là (<). Les efforts dits « intérieurs » ne le sont que par convention et n'interviendront que lorsqu'on les aura rendus extérieurs en considérant un sous-système.
Le Postulat de Cauchy ==>>
C'est l'hypothèse fondatrice de la Mécanique des Milieux Continus − la seule en fait pour la théorie générale, tout le reste sera plus ou moins déductif jusqu'à l'écriture des lois de comportement qui particulariseront ensuite le modèle pour l'appliquer à divers matériaux −.
Les efforts sont de deux types :
- à l'intérieur, forces de volume : f dm = ρ f dv .
- à la frontière, efforts surfaciques : T dS .
Ce postulat introduit, à côté des efforts volumiques (pesanteur en général), le vecteur contrainte T(x,t;n), force par unité de surface exercée au point x et au temps t au travers d'un élément de surface de normale extérieure n (« facette »).
Equations du mouvement ==>>
La loi fondamentale s'écrit alors
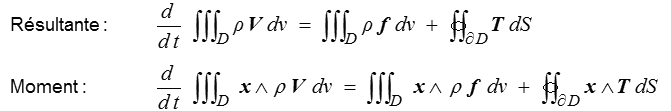
valable pour tout système matériel donc pour tout domaine D.
On peut caractériser la dépendance du vecteur contrainte T par rapport à la normale n en apppliquant la résultante de la loi fondamentale à des domaines particuliers :
- à un disque plat : T est fonction impaire de n,
- à un tétraèdre : T dépend linéairement de n.
L'état de contraintes en un point est donc entièrement défini par une application linéaire :
T = σ n, σ : Tenseur des Contraintes .
On peut maintenant exploiter complètement la loi fondamentale (résultante et moment) et obtenir ainsi l'équation du mouvement
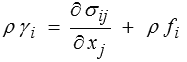
ainsi que la symétrie du tenseur des contraintes.
Le Tenseur des contraintes ==>>
Pratiquement, pour manipuler les tenseurs comme les vecteurs on utilisera un repère cartésien orthonormé, les « calculs tensoriels » se réduiront alors à du banal calcul matriciel (<) .
On peut alors succesivement :
- Interpréter les composantes du tenseurs des contraintes
- sur la diagonale : contraintes normales,
- en dehors de la diagonale : contraintes de cisaillement.
- Diagonaliser le tenseur des contraintes et introduire les contraintes principales.
- Décomposer le tenseur des contraintes en partie sphérique et déviateur.
- Etablir les formules de changement de repère.
- etc.....
Représentations Géométriques ==>>
Différentes représentations géométriques sont traditionnellement introduites :
- Ellipsoïde de Lamé,
- Quadrique directrice des contraintes normales,
- Espace des contraintes principales,
- Représentation de Mohr.
Pour un état de contrainte plan, cette dernière est particulièrement importante et conduit au Cercle de Mohr des contraintes.(>)
