Flexion pure
Un champ de contrainte
Considérons le champ de contrainte défini dans un système de coordonnées cartésiennes (x1, x2, x3 ) par
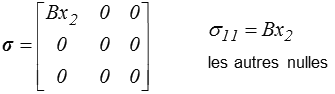
Comme pour la torsion les équations d'équilibre sont vérifiées et nous allons caractériser les efforts exercés sur un barreau rectangulaire de hauteur h, largeur b, et longueur l (pour fixer les idées ; contrairement au cas de la torsion, la forme du barreau n'a ici aucune importance).
Comme en torsion, la surface latérale (n1 = 0) est libre de contrainte (car le vecteur normal est dans le plan x2, x3), et il suffit d'étudier les deux sections d'extrémités, x1 = l par exemple,
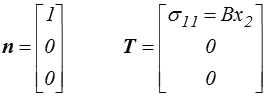
La section x1 = l est donc soumise à une contrainte normale fonction linéaire de x2.
Le torseur résultant se calcule directement
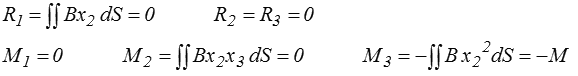
La seule composante non nulle est
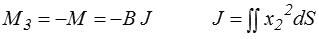
où J est appelé moment d'inertie (géométrique, pour être plus précis et éviter la confusion avec les moments d'inertie de la mécanique du solide rigide en rotation) par rapport à l'axe x3.
Pour la section rectangulaire considérée ici
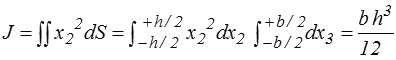
On trouve de même sur la section x1 = 0 un couple opposé.
Notre barreau est donc soumis à l'action d'un couple autour de x3. C'est ce que l'on appelle une sollicitation de flexion.
Champ de déformation
Contrairement à ce qui se passait en torsion, ni l'intuition, ni l'expérimentation ne nous permettent de deviner la structure du champ de déplacement.
Pour aller plus loin il nous faut anticiper un peu : le champ de contrainte postulé plus haut, et qui peut, au moins dans certains cas, décrire la flexion, correspond à une contrainte élémentaire de traction simple (<) . Le tenseur de déformation y aura donc la forme correspondante
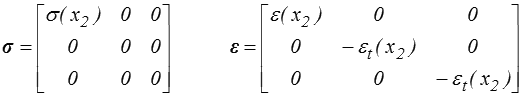
Certes cette sollicitation dépend de la position x2, mais cela n'influe guère sur la loi de comportement qui, en chaque point, exprime une relation locale entre contraintes et déformations.
Nous prenons comme hypothèse de travail une relation linéaire entre contraintes et déformations (c'est en fait l'élasticité linéaire que nous développerons plus loin). Puisque σ est linéaire en x2, les déformations ε et εt le seront également, nous écrirons donc
ε = κ x2 εt = β κ x2
où β et κ sont deux constantes dont nous dégagerons plus loin la signification. Nous tentons donc de prendre
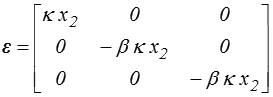
Nous constatons ici que (comme en torsion), ce champ de déformation étant linéaire en x2 , il vérifie donc les équations de compatibilité. Toutefois, et contrairement au cas de la torsion, cette vérification est ici cruciale car elle nous garantit l'existence (non postulée au départ) d'un champ de déplacement.
Calcul du déplacement
Nous avons donné (<) la forme générale du déplacement associé à un champ de déformation linéaire. Il suffirait donc d'appliquer ce résultat. Nous allons cependant − à titre d'exercice − faire ce calcul directement.
Les équations différentielles vérifiées par les déplacements sont
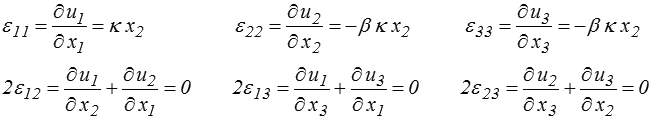
L'intégration de la première équation donne
u1 = κ x1x2 + φ1 (x2 , x3 )
avec une « constante d'intégration » φ1 fonction de x2 et x3 puisque nous avons intégré en x1. Les deux équations suivantes donnent de même
u2 = −½ β κ x22 + φ2 (x1 , x3 ) u3 = − β κ x2 x3 + φ3 (x1 , x2 )
Il faut maintenant reporter ces expressions dans les 3 équations suivantes. On obtient ainsi
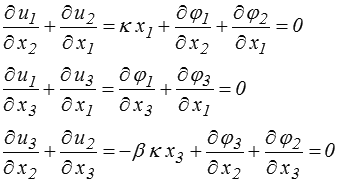
Rappelons que, dans la démarche générale, il suffit de trouver une solution particulière. En examinant ces équations, on remarque que seul le terme en φ2 peut dépendre de x1 dans la première équation et de x3 dans la troisième. Une solution particulière sera donc
φ1 = φ3 = 0 φ2 = ½ κ (−x12 + β x32 )
Le champ de déplacement sera donc, à un déplacement de solide rigide près,
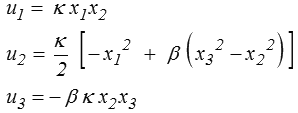
expression que l'on aurait effectivement été bien incapable de deviner a priori.
Interprétation de cette solution
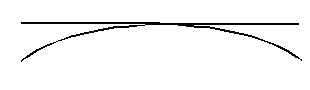Considérons la fibre moyenne (c'est-à-dire l'axe x1 lieu des centres géométriques de toutes les sections x1 = Cte). Sa déformée est donnée par (x2 = 0, x3 = 0)
u1 = u3 = 0 u2 = −½ κ x12 = v (x1 )
C'est une parabole, et κ est la courbure ; la flexion induit une courbure, ce qui confirme l'expérimentation. En réalité, c'est même un cercle qui, dans le cadre de l'hypothèse des petites perturbations peut être assimilé à une parabole. On parle souvent de flexion circulaire.
Si l'on examine maintenant le mouvement d'une section droite x1 = Cte, on constate que le déplacement u1 est proportionnel à x2, ce qui correspond à une rotation d'angle κ x1 , qui se trouve également être l'angle (−∂v / ∂x1 ) de la tangente à la fibre moyenne déformée.
On constate donc
Hypothèse de Navier Bernoulli.
Les sections planes restent planes et normales à la fibre moyenne déformée.
Théorie approchée de la flexion
Cette propriété que nous avons ici obtenue de manière un peu artificielle sera en fait « démontrée » en élasticité. De manière plus générale, elle reste largement acceptable et fournit une approximation très correcte pour l'étude de la flexion.
Cette théorie approchée est donc basée sur les deux hypothèses suivantes.
Hypothèse 1.
L'état de contrainte est localement de traction simple
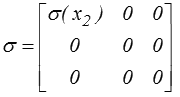
Hypothèse 2.
L'allongement longitudinal ε = ε11 est fonction linéaire de x2
ε = κ x2 (κ : courbure)
Il suffit alors de connaître le comportement du matériau en traction simple pour en tirer, en fonction de la courbure, la répartition des contraintes σ(x2) puis, par intégration, le moment.
Nous pouvons remarquer que, comme en torsion, nous avons obtenu en première analyse une répartition linéaire pour les contraintes et les déformations, ce qui est normal pour un comportement linéaire. Si tel n'est plus le cas, cela ne peut plus fonctionner, et on ne peut avoir simultanément linéarité des contraintes et des déformations. Les équations de compatibilité nous confortent alors dans l'idée de conserver la linéarité pour les déformations (et donc de la perdre pour les contraintes).
Traction et flexion composée
De façon plus générale, on peut étendre le modèle approché présenté plus haut en généralisant l'hypothèse 2.
Hypothèse 2'.
ε = εo + K x2 + L x3
où εo est l'allongement de la fibre moyenne, et K et L les courbures dans les deux plans. La loi de comportement donnera alors la contrainte σ(x2 , x3 ) puis par intégration le torseur des efforts appliqués sur la section d'extrémité
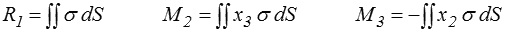
les autres composantes étant nulles. Ceci correspond à une sollicitation de traction R1 superposée à une flexion autour des deux axes x2 et x3.
Pour une section rectangulaire, et plus généralement pour une section doublement symétrique, ces sollicitations sont découplées. Divers couplages peuvent exister si tel n'est pas le cas.