Représentations géométriques des contraintes
Pour qui découvre la Mécanique des Milieux Continus, la difficulté majeure est assurément la notion de tenseur, c'est-à-dire de grandeurs physiques premières représentées par une application linéaire ou une forme quadratique. Diverses représentations géométriques permettent de mieux les « voir » et de s'en construire une perception intuitive.
Quadriques des contraintes ===>
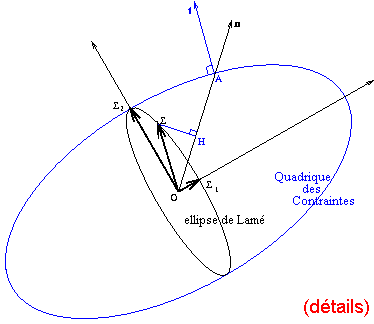L'ellipsoïde de Lamé est, dans l'espace physique, le lieu de l'extrémité du vecteur contrainte lorsque tourne le vecteur n (normale à la facette).
C'est un ellipsoïde dont les axes sont les directions principales du tenseur des contraintes et les demi-axes les contraintes normales principales.
La quadrique directrice des contraintes est la quadrique d'équation
x .σ x = σij xi xj = 1
Elle donne directement la direction du vecteur contrainte associé à la normale n (et un peu moins directement son module).
Espace des contraintes principales
Si l'on s'intéresse uniquement aux contraintes principales, un état de contrainte sera représenté par un point Σ = ( σ1 , σ2 , σ3 ) dans l'espace (supposé euclidien, mais sans lien avec l'espace physique) des contraintes principales.
Espace des Contraintes principales Plan déviatoire
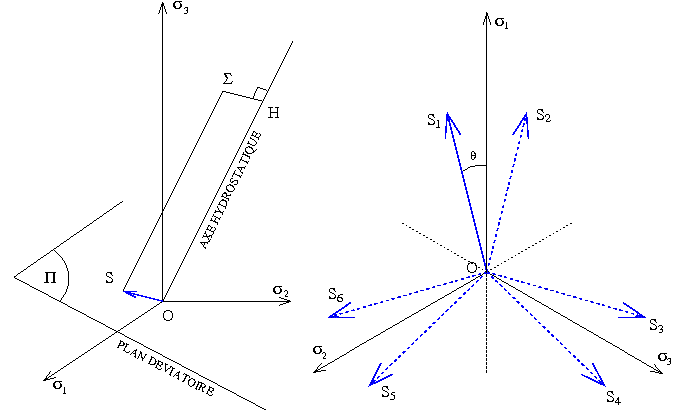
Cette représentation permet notamment de donner une interprétation géométrique des invariants ( σI, sII, sIII ) du tenseur des contraintes (<) ou de son déviateur : l'axe hydrostatique, trissectrice du trièdre, correspond aux états de contrainte isotropes ( σ = σ 1 ) tandis que le plan déviatoire, qui lui est perpendiculaire, correspond aux déviateurs. En notant respectivement H et S, les projections du point Σ sur l'axe hydrostatique et sur le plan déviatoire, on peut montrer simplement que
| OH | = σI /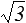 
| OS |2 = | s |2 = −2 sII
et, plus laborieusement, que cos 3θ est, à une constante près, donné par le rapport sIII / | s |3
Ainsi
- σI représente la partie sphérique du tenseur des contraintes,
- sII et sIII représentent le module et l'orientation du vecteur OS dans le plan déviatoire.
On remarque en particulier que ces relations donnent cos 3θ et ne déterminent donc l'angle θ, parfois appelé - je ne sais pas trop pourquoi - angle de phase, qu'au signe près et modulo 2π / 3. Ceci correspond au fait que seul est défini le triplet non ordonné des contraintes principales. Un état de contrainte est donc, dans le plan déviatoire, représenté par 6 points équivalents.
On peut par exemple se limiter au secteur 0 ≤ θ ≤ π / 6 et compléter par symétrie.
Représentation de Mohr
La représentation de Mohr montre l'évolution des contraintes normales et tangentielles lorsque l'on fait tourner la facettte n.
Le Plan de Mohr a pour abscisse la contrainte normale (algébrique donc) et pour ordonnée la contrainte tangentielle.
Dans le cas tridimensionel cette contrainte tangentielle est un vecteur dont on prendra la norme. On arrive ainsi au Tricercle de Mohr défini à partir des 3 contraintes principales σ1, σ2 et σ3 :
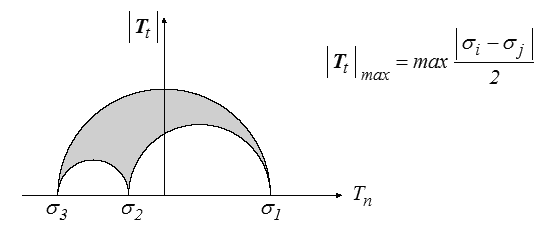
On montre sans difficulté que le point représentatif du vecteur contraintes décrit, lorsque la normale n varie, le domaine grisé.
Il en résulte en particulier que la contrainte tangentielle maximale vaut la demi différence des contraintes principales extrêmes.
Dans le cas bidimensionnel on choisit d'orienter la contrainte tangentielle Tt à +π /2 de Tn.
On construit ainsi le Cercle de Mohr des Contraintes ===>.